搜索
关闭

拥堵的动力学——城市交通网络建模的前世今生
发布时间:2021-05-24
一、引言
拥堵无时不有,塞车无处不在。持续数小时乃至数天的交通拥堵(Congestion)不仅出现在各种影视或文学作品中,在现实生活中也已经是司空见惯了。当实际车辆数量超出了道路所能承载的车辆数目上限,拥堵便会发生。随着城市化进程的加速推进,城市道路网承载能力有限与交通需求快速增长的矛盾日益突出,而道路交通拥堵所导致的通勤时间过长已经成为大城市居民和政府所要面对的关键问题。在这一语境下,对交通拥堵这一复杂的时空现象进行识别、描述和控制已经成为研究的热门领域(图 1)。城市道路构成相互连接的二维乃至三维网络,行人和各类车辆的行为具有高度的独立性、利己性和不可预测性,以及出发点-目的地(Origin–destination,OD)组合的多样性,使得从动力学上刻画交通拥堵现象尤为困难。但万幸的是,大数据时代的到来使得我们能够广泛使用 GPS 等实时数据对交通拥堵的具体过程进行基于个体而非统计指标的精细描绘,标志着对交通拥堵的动力学研究迈上了一个新的台阶。
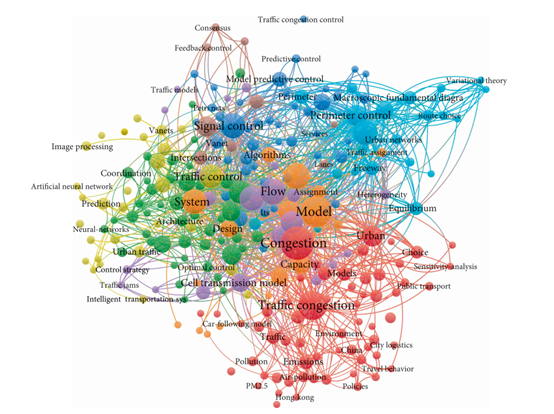
图1 交通拥堵研究的关键词共生网络【1】
交通拥堵动力学致力于在大型城市道路交通网络中对交通拥堵的产生、时空传播和消弭进行建模。具体而言,拥堵动力学关注一个城市交通网络的宏观基本图(Macroscopic Fundamental Diagram,MFD)。这一概念最早由Daganzo和Geroliminis【2】提出,认为MFD描述的是交通网络中车流密度和车流量的关系,并在许多交通网络中进行了观测和验证。MFD是在网络层面被构建的,与具体单个链接上的车流量、车流密度和速度所构成的基本图(Fundamental Diagram,FD)并不相同。但是,获得各个节点、链接上的基本图对于MFD的构建仍是有意义的,而各个FD之间的时空异质性可能正是解开MFD之谜的钥匙。MFD与交通拥堵的关系很简单,即当车流密度增加到一定程度时,车流量便会随着车流密度的增加而降低,这个时候就是我们常说的交通拥堵状态了。当然,对于网络中的各个车道和交叉路口,我们可以简单地认为当车流速度小于某个阈值时为交通拥堵,如果车流速度为零,则表明该车道或交叉路口彻底堵塞。大规模的堵塞则会导致整个交通网络的崩溃。
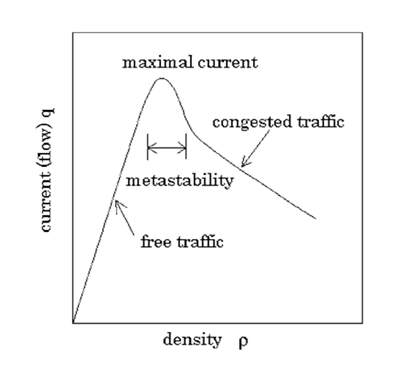
图2 宏观基本图描述了车流密度和流量的基本关系【3】
二、交通拥堵的模型构建
交通系统是一个典型的多体复杂系统。正如在其他领域(如生态学、流行病学、统计物理等)问题中所采取的手段那样,对交通流的建模也可以在多种尺度和不同的概念框架下进行,在本文中,我们将介绍三类典型的交通拥堵模型,即微观尺度的模型、宏观尺度的模型和中等尺度的模型。
1. 微观尺度的模型
微观尺度模型,是以车辆本身为单位构建的模型。在这些模型中,城市交通网被认为是一个远离平衡态的多粒子系统。
1.1 跟驰模型
跟驰模型(Car-following model)是一种典型的微观模型。早在1961年,Newell【4】就提出,在同一车道上,一辆汽车的运动状态仅仅取决于同方向在它之前的那辆车(也称为leading car)而与其它车辆无关。如果这辆车和它的前车分别用车辆j和j+1来表示,我们可以用以下的微分方程来表示j车的运动状态:
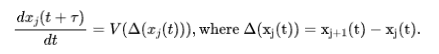
这里的函数 被Newell称为最优速度(Optimal Velocity),因此该模型也被称为最优速度模型。表明 车的运动状态和 与 两车的距离之差有关,因此 显然应该是 的单调递增函数,如Bando等人提出 可以是双曲正切函数的形式【5】。跟驰模型十分简单,在理论分析和实验模拟上都很方便。但是过度简化的假设导致该模型无法精确刻画现实路网中的复杂情形。最直观地,如果 车由于某些原因突然减速,那么 车很可能无法在时间 内进行反应并避免碰撞的发生。此外,基于个体的模型和预测大规模交通网络的动态之间还存在着巨大的鸿沟。据此,这一模型也正在被不断修正和扩展,如考虑多种不同车辆类型【6】、引入随机性【7】等等。
1.2 元胞自动机模型
元胞自动机(Cellular Automata,CA)是模拟多粒子物理系统时空演化的有力手段。事实上,第一个将元胞自动机用于交通模拟的正是元胞自动机的开创者之一,著名数学物理学家和企业家Wolfram【8】。在CA模型中最基本的假设是:一辆汽车前方如果没有被其他车辆占据,那么该车将在下一个时刻移动到该位置。在整个系统中,所有车辆的位置都依此法则被同步更新。具体而言,其动力学模型可由下式表示【9】:
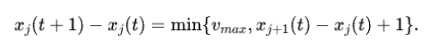
不难证明,在一定条件下这一CA模型和上文中的跟驰模型是等价的【3】。
同跟驰模型一样,CA模型也面临着过度简化的缺陷,但仍然被认为是大规模模拟现实交通流的先驱。近年来,CA模型也有了极大的改进,如2018年,Olmos等【10】基于改良的CA模型和真实道路网格,动态刻画了交通网络在高峰期时的脆弱性。在该文章中,每个车辆从交叉口出发,并根据路由策略汇入网络。在交叉路口处,车辆会降低其速度并动态保持与前车的距离。由此,作者能够从微观角度模拟交通网络在自由流动、交通堵塞和网络崩溃之间的切换(图3)。
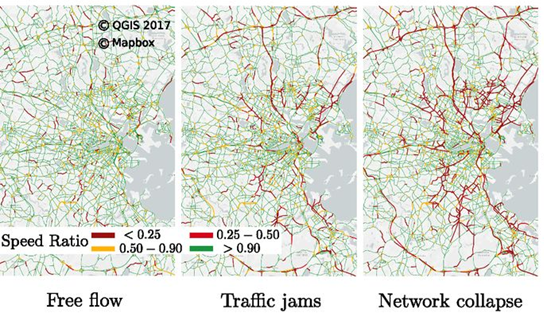
图3 使用CA模型模拟波士顿的交通动态,从左至右表明了整个交通网从自由流动到交通网络崩溃的过程。
天然的模型假设和车辆行程逻辑是任何微观尺度模型的开发者和使用者所必须小心考虑的问题,也是最有可能被人诟病之处。但微观模型的存在使得大规模模拟城市交通网络成为了可能。得益于分布式计算的飞速发展和模型的不断细化,通过微观模拟还原MFD或许会成为相关领域研究的主流方法。此外,类似算法已经在各类模拟软件、游戏中广泛使用,如基于Unity引擎开发的模拟经营类游戏《都市:天际线》(Cities: Skylines)中,已经能够借助游戏引擎实现基于游戏内道路交通网络的数以万计的车辆和行人的并行模拟并按照玩家指令进行行动(图4)。这种模拟对于今后研究,尤其是对于近年来提出的以所谓“智慧城市”为实现目标的研究领域具有重要意义。

图4 游戏《都市:天际线》中借由游戏引擎模拟的车流,但由于游戏内置的车辆行为逻辑还不完善,导致城市拥堵时有发生,因此该游戏也被玩家们戏称为“堵车天际线”。
2. 宏观尺度的模型(Macroscopic Models)
宏观交通模型力图从全局角度刻画车流量和车辆密度的时空分布,而不关心具体某一车辆或行人的行为逻辑。对于这类模型,微分方程自然成为了最好的描述手段。在宏观交通模型中,最常见的当属流体模型。城市交通系统的流体模型认为整个系统是一个一维可压缩流场,而车辆行驶的过程就可以类比于流体扩散的过程。对于交通系统中的每个位置 和时间点 ,流体力学中的连续性方程告诉我们车流密度 和车流量 之间存在如下关系:
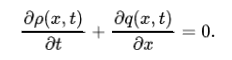
当然,仅靠这一个方程不足以同时解出流量和密度这两个变量,必须对其施加其他的限制。比如提出该模型的Lighthill和Whitnam就认为流量 应该由基本图FD和一个小的扩散项决定等【11】。后来,流体模型也被不断细化,如考虑从匝道汇入主干道的车流【12】,将模型扩展到二维道路网等等【13】。当前所使用的流体模型也主要基于其二维形式。从流体模型出发很容易得到MFD,且容易从方程本身出发分析其稳定性。但是,流体模型由于假定了一个在大范围内适用的微分方程(组),其对于细节的刻画程度自然远不如各种微观尺度的模型。此外,大多数流体模型都局限于二维网格而非网络。前者与后者的最大差异在于网格的节点被完全限制在整数格点上,而忽略了城市交通路网可能出现的各种差异性结构。
3. 中等尺度的模型——沟通微观与宏观的桥梁
中等尺度模型,或曰介观模型(Mesoscale models),其所描述的主要对象不同于微观模型中的每一个车辆,也不同于宏观模型中的整个交通系统各个点的状态,而是网络中的各个基本元素,如道路、交叉路口或一些车辆的集群。这类模型的目的,不在于精确描述系统中各个车辆通过各个道路或交叉路口时的速度,而在于复现网络的整体特征,比如车辆速度的分布、拥堵的时空演变等等,这对于刻画拥堵时的MFD是必要的。中尺度模型最早可以追溯到上世纪70-90年代提出的各种气体动力学(Gas-Kinetic)模型【14】。这些模型起源于流体模型,同样认为城市交通网是一个被物理学定律支配的系统。但如果我们将建模的对象限制在网络结构内部,如网络节点或连边,而点与点之间的相互作用受到物理定律的影响,就可以得到介于微观与宏观之间的模型。这里所谓的“物理定律”可以被归结于以下两方面:其一,如果一条道路或一个交叉口出现了拥堵,司机会倾向于改走与该道路或交叉口相邻的道路中的一条;其二,如果一个交叉口的临近交叉口都是拥堵的,那么拥堵状态会很容易地传播到这个交叉口。这两条原则是人们驾车时选择行驶路线的天然逻辑,因而也构成了中尺度模型的基本构建原则。以下我们介绍近两年来发展出的两种中尺度模型,分别是传染病模型和反应-扩散模型。
3.1 传染病模型
将交通拥堵传播的过程类比传染病在人群中的传播过程是一种十分自然的想法。早在2004年,就有学者认为拥堵的传播可以用网络上的易感者-感染者-恢复者(SIR)模型来描述【15】,而2020年Seberi等人的一篇文章中为该模型提供了经验证据【16】。这里,拥堵传播网络中的节点即为现实网络中的交叉路口,而节点之间的连边即为交叉口之间的道路。该模型假设对于一个已经处在拥堵状态的节点,其邻近的节点都可能成为下一时刻被传染的目标,而已经拥堵的节点将在一段时间后恢复正常。这里,所谓处于拥堵状态是指某条道路上的车辆瞬时速度与观测到的最大速度的比例小于某个阈值。Seberi等人提出的传染病模型的基本方程如下:
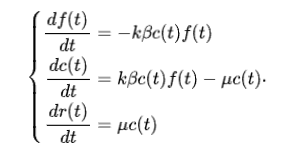
其中, 分别描述了处在自由流动(Free traffic)、拥堵(Congested)和恢复(Recovered)状态的道路的比例。在文献【16】中,作者考察了六个不同城市中拥堵的传播和消散动态并估计了模型参数,其模拟结果与实际结果符合地很好(图5)。此外,作者还通过建立空模型(Null-model)考察了拥堵的来源,认为某条道路发生拥堵有赖于上游拥堵集群的形成。
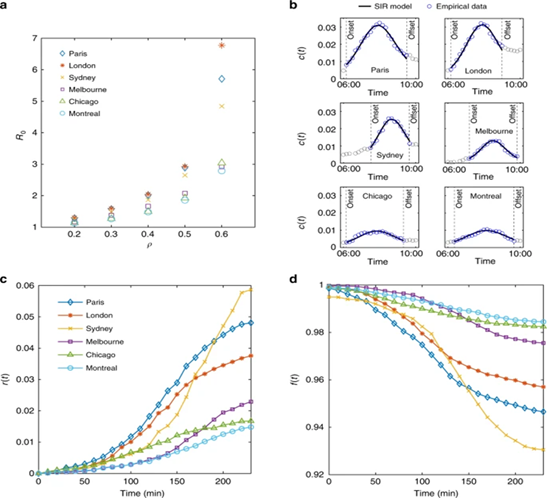
图5 使用SIR传染病模型刻画不同城市的道路交通拥堵【16】。a:在六个不同城市中,道路拥堵传播的“基本再生数”(Basic Reproduction Number, );b:不同城市的参数拟合结果。蓝色实线表示模拟结果,白色圆圈为观测数据;cd:不同城市中道路的自由流动和拥堵恢复状况随时间的变化。
传染病模型的特点在于较为简单且高效,同时集成了微观与宏观模型的长处,既能考察某一特定道路上的车流动态,又能识别全局交通拥堵的概貌。但是,将交通拥堵与SIR传染病模型进行全盘类比可能是一个不严格的假设。如,模型中假定了一个拥堵的交叉口或道路之后会自行恢复为不会再拥堵的状态,而这与现实交通网络随时可能爆发的拥堵或许是相悖的。当然,作者在文中指出“宏观层面上假设当一个环节从拥堵中恢复时,直到下一个高峰期才会再次拥堵,这也许不是没有道理的”。但或许需要引入更多的状态来完善模型,并考虑交通系统可能存在的周期性。
3.2 反应-扩散模型
反应-扩散(Reaction-Diffusion)模型早已成为物理学中的经典模型。基于上述的两条中尺度模型基本原则,我们也可以将其应用于城市交通路网。顾名思义,反应-扩散模型方程由一个反应项和一个扩散项组成,且分别对应于上述第二条和第一条原则。同传染病模型一样,反应-扩散模型也关注某条道路上的平均速度u_i (t),而拥堵状态则被定义为平均速度小于某个阈值。平均速度具体的变化规律由Bellocchi和Geroliminis在2020年提出【17】,可写为:
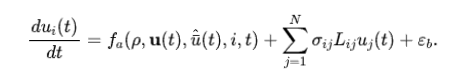
根据交通拥堵的两个传播原则和实际数据的特点,可以对反应项 、扩散项 和噪声项 的具体形式进行限定和细化。作者在文中给出了具体的函数形式,并使用深圳出租车实时GPS数据进行了参数校正。结果表明,使用反应-扩散模型能够以较高的精度还原真实的交通拥堵图景(图6)。此外,作者还研究了拥堵集群(一组平均速度低于阈值且相互连接的道路的集合)的分布和准拥塞期(quasi-congested,介于拥堵和自由流动之间的时期)所具有的性质。值得注意的是,在该研究中,作者将道路(链接)定义为交通网络中的节点,而将交叉路口定义为网络中的连边。这一定义似乎不符合我们对于真实交通网的直观印象(与上述SIR模型中的定义正好相反),但可以使得我们将道路上的平均速度视为节点的属性而非边的属性,因此在应用中是“简单而有用的”。然而,该研究目前还仅停留在对单个城市的出租车群体进行追踪和建模的层面上,虽然能够较为准确地刻画车流速度的时空变化,但由于缺少了私家车、公交车、货车等群体,其对于描述车流密度这一MFD中最关键的指标还无能为力。
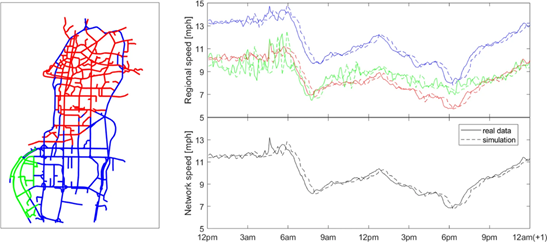
图6 在深圳的道路网中使用反应-扩散模型模拟出租车交通流量。左:将城市道路网分为不同区域,分别用三种颜色表示;右:不同区域的车流速度(右上)和整个网络的平均速度(右下)随时间的变化,模拟数据和真实数据分别用虚线和实线表示。
三、总结与展望
真实的城市道路交通网络千变万化,其时空异质性和复杂度远超人们的想象。因此,以当前的技术和算法而言,不论从任何尺度对城市交通拥堵进行建模的尝试都只能说是窥其冰山一角。然而,随着数据的精细化、算法的高效化和仿真环境的成熟化,我们对城市交通拥堵的理解亦当愈发深刻。就前景而言,笔者认为较有前景的、能够深度刻画交通拥堵结构和动态的模型应该会集中于微观和介观领域。前者得益于大规模并行计算算法和平台的成熟,搭载元胞自动机或类似模型,能够实现城市规模的道路交通实时仿真。而后者的优势在于将网络结构和拥堵传播的动力学有机结合起来,通过对真实世界的适当简化和建模,使我们能够掌握每条道路、每个交叉口的交通动态,从而能够有针对性地施加控制。而对于宏观尺度的模型而言,其对交通网络的栅格化和对交通规则的过度简化是其天然的弊病,因此其对于拥堵过程的刻画难免较为粗糙,但其优势在于能够快速地导出MFD和方便地引入控制项。
文:侯嘉文
【参考文献】
[1] Ma, C., Zhou, J., Xu, X. D. & Xu, J. Evolution regularity mining and gating control method of urban recurrent traffic congestion: a literature review. Journal of Advanced Transportation 2020(1), 1-13 (2020).
[2] Geroliminis, N. & Daganzo, C. F. Existence of urban-scale macroscopic fundamental diagrams: Some experimental findings. Transportation Research Part B: Methodological 42(9), 759–770 (2008).
[3] Nagatani, T. The physics of traffic jams. Reports on Progress in Physics 65(9), 1331 (2002).
[4] Newell, G.F. Nonlinear Effects in the Dynamics of Car-Following. Operations Research 9, 209-229 (1961).
[5] Bando, M. et al. Dynamical Model of Traffic Congestion and Numerical Simulation. Physical Review E 51(2), 1035-1042 (1995).
[6] Xie, D. F., Gao, Z. Y., Zhao, X. M. & Li, K. P. Characteristics of mixed traffic flow with non-motorized vehicles and motorized vehicles at an unsignalized intersection. Physica A: Statistical Mechanics and its Applications 388(10), 2041-2050 (2009).
[7] Hamdar, S. H., Treiber, M. & Mahmassani, H. S. Calibration of a stochastic car-following model using trajectory data: exploration and model properties. Environmental Monitoring & Assessment 158(1-4), 479-498 (2009).
[8] Wolfram, S. Theory and applications of cellular automata (Advanced Series on Complex Systems) World Scientific Publication Singapore (1986).
[9] Fukui, M & Ishibashi, Y. Traffic Flow in 1D Cellular Automaton Model Including Cars Moving with High Speed. Journal of the Physical Society of Japan 65(6), 1868-1870 (1996).
[10] Olmos, L. E., Çolak, S., Shafiei, S., Saberi, M. & MC González. Macroscopic dynamics and the collapse of urban traffic. Proceedings of the National Academy of Sciences 115(50), 201800474 (2018).
[11] Lighthill, M.J. & Whitham, G.B. On Kinematic Waves. II. A Theory of Traffic Flow on Long Crowded Roads, Proceedings of the Royal Society of London Series A 229, 317-345 (1955).
[12] Lee, H. Y., Lee, H. W. & Kim, D. Empirical Phase Diagram of Traffic Flow on Highways with On-Ramps. Springer Berlin Heidelberg (2000).
[13] Li, L., Cheng, R. & Ge, H. New feedback control for a novel two-dimensional lattice hydrodynamic model considering driver's memory effect. Physica A: Statistical Mechanics and its Applications 561, 125295 (2021).
[14] Prigogine, I. & Herman, R. Kinetic Theory of Vehicular Traffic. Elsevier New York (1971).
[15] Wu, J., Gao, Z. & Sun, H. Simulation of traffic congestion with SIR model. Modern Physics Letters B 18, 1537–1542 (2004).
[16] Saberi, M., Hamedmoghadam, H., Ashfaq, M. et al. A simple contagion process describes spreading of traffic jams in urban networks. Nature Communications 11, 1616 (2020).
[17] Bellocchi, L., Geroliminis, N. Unraveling reaction-diffusion-like dynamics in urban congestion propagation: Insights from a large-scale road network. Scientific Reports 10, 4876 (2020).


 loading......
loading......