一、引言

         Neuron期刊在2017年6月发布了以“How Does the Brain Work?”为主题的特刊，共有12篇文章从不同角度描述大脑的工作机制[1]。简单来讲，大脑的运作可以归结为单个神经元的放电机制及神经元之间的交互作用。大脑的信息传递依靠电信号在神经元之间的传递，神经元在接受到电刺激后，若达到阈值就会产生动作电位以脉冲式的信号发放，否则会处于静息态，并且动作电位的最终水平与阈上刺激的强度无关，这种动作电位的特性被称为“全或无”。单个神经元的放电行为与计算机的二进制编码方式有很大的相似性，只有0（静息态）或1（动作电位）两种状态，类似于二进制编码对于计算机运作的作用，在计算神经科学中，神经信息的编码和解码对于神经活动的理解起着很重要的作用。当下一些传统的编码理论和解码技术[2-5]有着各自的应用场景，但同时又有各自的局限性，目前还没有一套完善有效的信息编码理论从全局角度分析大脑活动。大脑的神经结构和网络结构是复杂多层次的，而神经元是通过膜电位的非线性发放模式来决定神经活动的，因此从全局角度编码脑网络的神经信息就会遇到高维非线性耦合的难点。

         Hodgkin-Huxley(H-H)方程[6]严格精确地表示出了乌贼神经元的动力学行为，是目前研究实际神经元使用最为广泛的模型。假定H-H电路模型是一个描述神经元电学特性有效的工具，那么它同样可以有效地研究神经元的能量消耗特性。在H-H神经元模型中，膜电位函数和能量函数被证实有唯一的对应关系[7]，这保证了可以用能量来编码神经元的发放，进而编码大脑不同层次的神经活动。当脑网络产生了一种刺激，也就对应一种能量分布，这种能量分布即对这个刺激的编码[8,9]。能量是标量函数，因此神经元的能量消耗可以线性叠加[10]，这样就避免了神经元发放的非线性耦合，即更易于在全局的角度分析脑网络不同层次的神经活动。本文旨在总结阐述H-H模型下神经元的电学行为及其能量消耗特性。

二、H-H神经元模型

         H-H神经元模型[6]由Hodgkin和Huxley于1952年提出，该模型将神经元的膜电位变化为图1中的等价电路，各个离子通道的电流记为，，由基尔霍夫定律，通过细胞膜的总电流可以表示为：

  

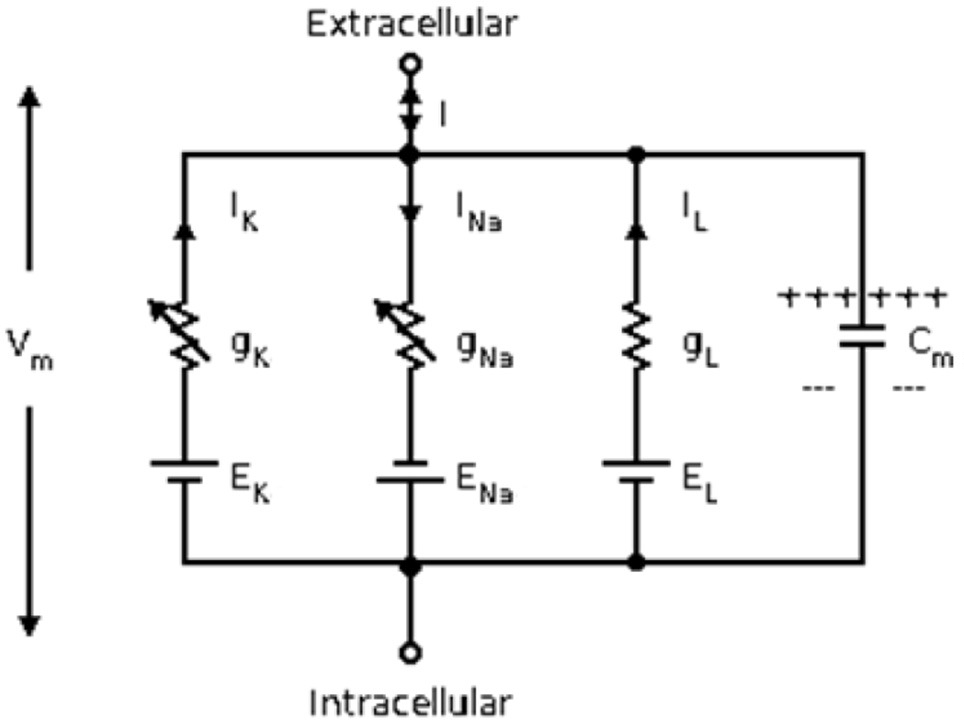
图1 Hodgkin-Huxley模型等价电路

各离子通道的电流可以用I_ion=g_ion（V_m - E_ion）表示，离子通道的导电强度g_ion与电压和时间都有关，可以表示为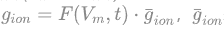，表示对应离子通道最大导电系数，F(V_m，t)是与膜电位和时间相关的通道函数，经过实验分析，可以得到以下方程：

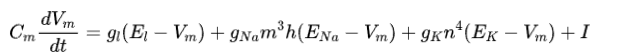
其中C_m表示膜电容量，V_m表示膜电位，E_Na和E_k分别表示钠离子和钾离子的能斯特电势，E₁表示泄漏电流为0时的电势。n、m、h表示离子通道打开的概率，分别满足以下微分方程：

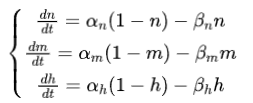
其中

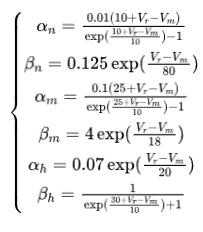
V_r表示静息电位。

考虑整个电路的能量，即等价电容器和电池的电势能总和[18]，可以表示为：

 

 

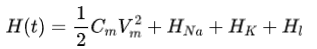
对应的功率为:

 

其中后三项为等价电池的功率，设为外部刺激电流，

 

 

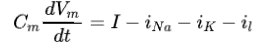
因此整个环路时刻的功率可以表示为

 

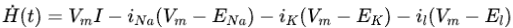
将离子通道电流表达式带入可以得到

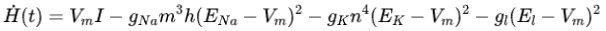
其中等式右边的第一项表示外部刺激电流的输入功率，后面三项分别表示离子通道的消耗功率

         给定总刺激电流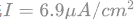，膜电位响应如图2(a)的脉冲信号，图2(b)为上式功率第一项VI，平均为正值且峰值到达600nJ / s，其能量来源于外部刺激电流 I。图2(c)为上式功率中的后三项，即离子通道消耗功率的总和，平均为负值且峰值到达100000nJ / s，远低于外部刺激电流的输入功率，这部分功率就需要ATP水解提供能量，同时离子泵主动运输保持离子电池的电势能。

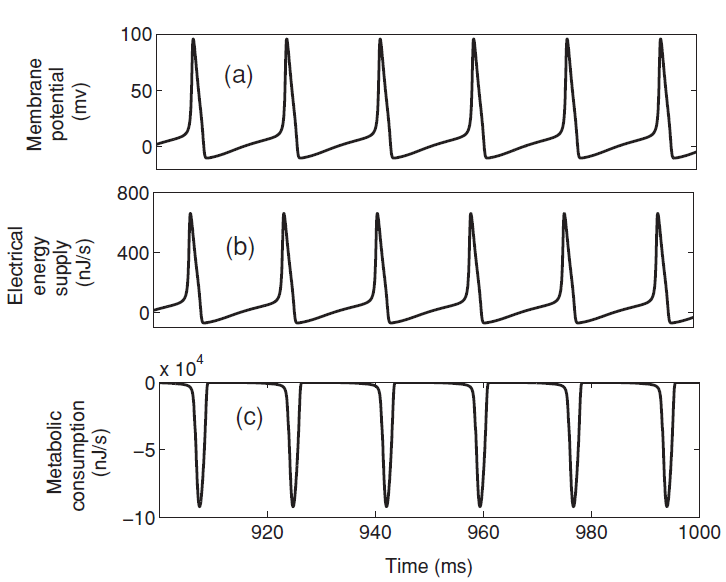
图2 动作电位膜电位和功率

图3展示了各个离子通道的电流以及功率，其中Na+离子与K+离子和泄漏电流方向相反，各离子通道功率均为负值但图3展示了正值便于观察。单个神经元产生一个动作电位的总能量消耗即这三部分能量的总和，描述的是离子被动运输的能量消耗，而重建膜电位所需要保持的细胞膜内外离子浓度依靠的是离子泵消耗ATP水解能量的主动运输。

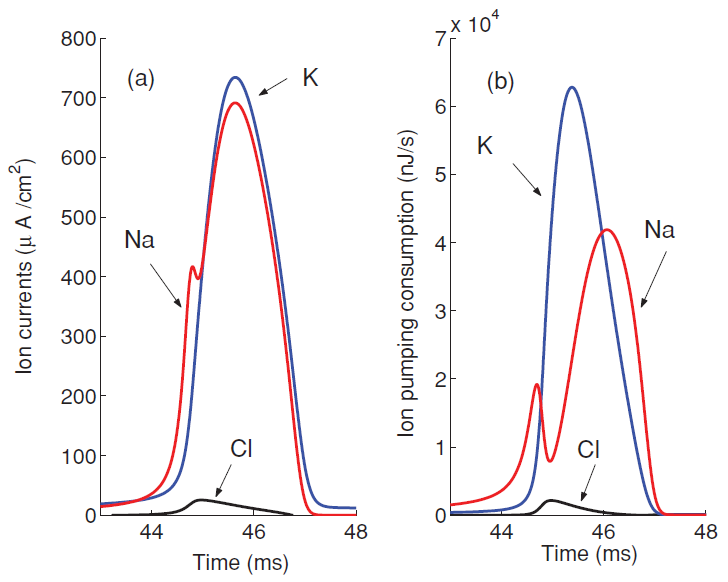
图3 离子通道电流和能量消耗

三、总结与展望

         由于大脑的认知神经结构是复杂多层次的，因此结合多尺度多层次的神经编码方式来研究大脑皮质是非常必要的。特别地，为了避免神经元之间高度非线性耦合性带来的困难，构建一个从全局角度出发的有效理论对理解大脑的运作方式起着极其关键的作用，因此能量作为一个宏观尺度的指标可以很好的刻画这方面的性质，但目前的方法仍未将神经元之间的耦合方式和网络结构在能量中体现出来，还需进一步探究相关性质。本文简单介绍了基于H-H模型的单个神经元的动作电位发放及能量消耗模式，后面将继续解析现有的能量编码方法以及对构建全局宏观指标方法的探究。

文：李舒旺

  

【参考文献】

[1] How does the brain work? Neuron. 94, 933–933. https://doi.org/10.1016/j.neuron.2017.05.030

[2] Amari, S., and Nakahara, H. (2005). Difficulty of singularity in population coding. Neural Comput. 17, 839–858. doi: 10.1162/0899766053429426.

[3] Purushothaman, G., and Bradley, D. C. (2005). Neural population code for fine perceptual decisions in area MT. Nat. Neurosci. 8, 99–106. doi: 10.1038/nn1373.

[4] Natarajan, R., Huys, Q. J. M., Dayan, P., and Zemel, R. S. (2008). Encoding and decoding spikes for dynamic stimuli. Neural Comput. 20, 2325–2360. doi: 10.1162/neco.2008.01-07-436

[5] Jacobs, A. L., Fridman, G., Douglas, R. M., Alam, N. M., Latham, P. E., Prusky, G. T., et al. (2009). Ruling out and ruling in neural codes. Proc. Natl. Acad. Sci. U.S.A. 106, 5936–5941. doi: 10.1073/pnas.0900573106.

[6] Hodgkin, Alan L., and Andrew F. Huxley. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of physiology 117.4 (1952): 500-544.

[7] Wang, R., Wang, Z. & Zhu, Z. The essence of neuronal activity from the consistency of two different neuron models. Nonlinear Dyn 92, 973–982 (2018). https://doi.org/10.1007/s11071-018-4103-7.

[8] Wang, Z., Wang, R. Energy distribution property and energy coding of a structural neural network. Frontiers in Computational Neuroscience, 2014, https://doi.org/10.1007/s11071-018-4103-7.

[9] Wang, Z., Wang, R., Fang, R. Energy coding in neural network with inhibitory neurons. Cognitive Neurodynamics, 2015, 9(2): 129-144.

[10] Wang, R., Zhang, Z., Chen, G. Energy function and energy evolution on neural populations. IEEE Transactions on Neural Networks, 2008, 19(3): 535-538.

[11] Moujahid, A., D’Anjou, A., Torrealdea, F. J., and Torrealdea, F. (2011). Energy and information in hodgkin-huxley neurons. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 83(3Pt 1):031912. doi: 10.1103/PhysRevE.83.031912.