搜索
关闭

用于神经形态计算的三阶纳米级电路元件
发布时间:2021-08-03
本文内容较多,简单将主要内容总结如下:
1、制备一种高性能的包含忆阻器的基本电路元素,从而在实际的器件性能测试层面表现出许多复杂的特性,讨论了一下其转变的机制。
2、基于前面其他的工作和前文的机制转变结论给出了一种描述该器件的数学模型,由于实质上包含三个物理量的对时间微分项,因而整个电路模型实质上是一个三阶的电路,并说明了数学模型上三阶的电路方程才能描述出一些复杂的现象。
3、用三个电路元素构成了一个简单的逻辑电路,其中整个电路的逻辑可以简单的通过改变其中一个电阻值实现改变。
4、用制备得到的该电路元素设计了一个模拟计算的实例,用来说明某些场景下使用忆阻器构成的神经形态计算相对于传统和量子计算具有优势。提出可以用这种实例作为类脑计算的一个性能检验标准。
忆阻器是什么
对于很多人而言,忆阻器这一名词可能是第一次听说。笔者在这里做一下介绍。
忆阻器,全称“记忆电阻器”,从名字可以看出命名者认为这应该是一种具有记忆功能的电阻。至于何为“记忆功能”还不大看出。倘若要讨论这个器件到底是为何物、有何用途,还需要联想一下其他的电路元件。
大家在对电路知识广泛认知中,电路中有3种基本的“无源”器件,分别是电阻、电容和电感。无源指的是他们本身没有电源提供能量(听起来有些奇怪),再换言说就是我们可以很简单的做出来这些没有电源的器件。设想一下,最简单的制作一个电容,就是找两个金属板相对靠近且不互相贴近;电感可以用一截铜导线卷成弹簧的样子;最简单制作的就属电阻了,在身边随便找一个导电性不强的物品,很多时候可以直接用两段导线直接接起来做个电阻。在做这些器件的时候,我们通常不会有塞个电源进去的想法,对吧?这也正是对无源器件的最本质的定义——里面没有任何电源。
再仔细看这三个无源器件,我们可以将电阻写成电压对电流求导的形式(电压和电阻的微商形式):
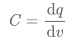
电容可以写成电荷和电压的微商形式:
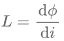
电感可以写成磁通量和电流的微商形式:
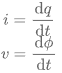
另外,电流和电荷、电压和磁通量两组关系本身又是时间上的导数-积分关系:
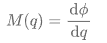
看到这里,是不是感觉缺少了一个东西呢?上面总共有四个物理量,不看两个导数积分关系,剩余的三个好像也没有构成某种旋转对称性是不是?这里,是不是觉得再补上一个磁通量和电荷的微商关系,就能够填补上这种旋转对称性了呢?在1971年,蔡少棠(Leon. O.Chua)注意到了这点,在数学上提出应该存在一个单一的无源器件,填补剩下的微商关系,并用M来标记这组微商关系,即

这里的M实际上就与我们现在称所称的“忆阻器”相对应。具体这个器件为什么被称为“忆阻器”,也就显而易见啦。作为磁通量和电荷的微商,M天生就是电荷的函数,如果对微商的分子分母同时除以dt,即上下都是对时间的导数,我们就能够得到
可见,M具有的是电阻的量纲。然而,M同时又是电荷量(指的是通过其上的电荷量)的函数,这样一来,M就是一个能够记录其上流过的电荷的,阻值一直处于变化当中的“电阻”,因此得名——忆阻器。
然而,在Chua的设想中,忆阻器应该是一个无源器件,但是在自然界中真实简单地再现这种功能并不容易。忆阻器的相关研究一直到2008年,才再次迎来曙光。惠普实验室的R. Stanley. Williams等人通过简单的小尺度制作,做出了Pt-TiO2-Pt结构的一个器件,其电学性能显示它的电阻值有随着电荷量的改变而改变的现象,他们认为这应该就是那个被称作“忆阻器”的东西,以“找到了失踪的忆阻器”为题发表了他们的报告,掀起了忆阻器的研究热潮。
不过,忆阻器也不都是一样的。事实上,相对于另外三个无源器件,忆阻器的行为和特性可以说是千奇百怪。最简单来说(也是本人所了解的两种,当然还有更多种)我们可以找到两种特性非常不同的忆阻器,一个是前面提及的TiO2忆阻器,阻值会随着通电而改变,有一定的记忆和保持能力;另一个就是本文即将要介绍的阈值转变器件,特征是会随着两端电压的增加在某个点发生阻值的转变,而电压慢慢降低时会在另一处发生反向的阻值转变,其性能是易失性的。通常而言,忆阻器可以用于生物神经元的模拟,非易失的可以用于模拟突触,易失的可以用于模拟神经元。突触的模拟原理这里不再加以描述,后面有机会我会找一篇突触相关的文章做介绍。关于阈值转变器件,下面我们直接进入本文的正题,介绍阈值转变器件的神经元模拟。
器件的结构和制备
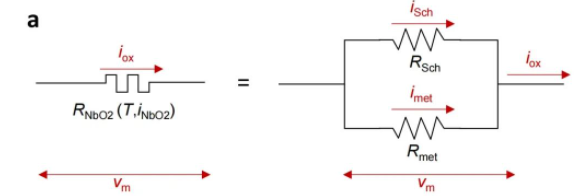
本文中涉及的 ‘element’ 结构都如下图(a,b,c)所示;上图(a)为的等效电路图,下图(b)为器件的结构。(后无特殊说明,element都指的是下面蓝框内的器件组合子电路,一般不短路Rint)

整个器件的制备是在12inch的硅晶圆上进行的。首先沉积W,而后沉积SiNx,SiNx作为后续沉积SiO2时对W电极(SiO2沉积涉及氧气,不做保护会对W有氧化)的保护。而后在其上沉积SiO2。通过euv光刻在SiO2层上制作2μm到50nm的通孔(对应图中长且稍窄的蓝色TiN部分)。掩膜版均为方块性,但是由于图案的变形导致100nm下均变成类似圆形。通过反应离子刻蚀制作直达底层W电极的通孔,在通孔中填入TiN。而后做抛光处理,再在其上沉积NbOx层。而后再结合光刻制作TiN层和Pt层。最后在稍大的电极上沉积一层5nm的Ti层,并破真空和再沉积Pt。Ti在真空中的氧化足够使其变成想要的电阻。对于器件而言,上下与TiN电极接触的NbOx和电极共同构成了element中的忆阻器,与SiO2接触的部分由于没有电荷的通过,因而不会有重要的忆阻器的特性的体现,而是构成了电容器的电介质的一部分。因而整体的等效电路图如图a所示。
转变机制
HP实验室的这部分研究人员之前也做过大量的关于NbOx忆阻器的研究。来自本文中的下图展现了扫描电流时整个element的i-v特性。
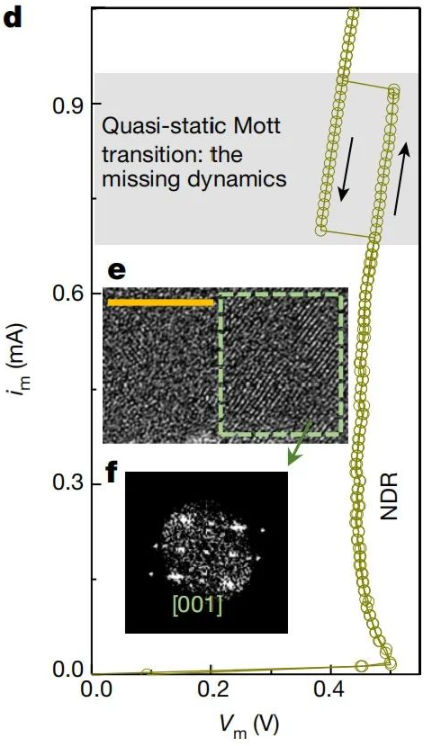
在对im进行扫描的过程中(im作为自变量随时间线性变化)element的电压vm有着不同的数值。对整个i-v特性来看,有两个区域表现出了不同的负微分电阻(NDR)特性。负微分电阻指的是对于某些电学元件,其整体的i-v或者u-i曲线会存在局部的斜率小于0的部分,即du/di<0。在他们之前的另一篇文章中(doi:10.1038/nature23307)他们对这两个NDR区做了分类和研究。他们将下方的类S型区域的NDR区成为NDR-1区域,将上方出现回线或者称为箱型曲线(box-shaped)的区域称为NDR-2区域。研究发现,NDR-1区域是400K左右的(电流控制的)非线性(热)输运导致的;NDR-2区域则是由1000K左右的(温度控制的)Mott 金属-绝缘体-转变(metal-insulator-transition,MIT)导致的,其中转变后的金属态的热导要弱于绝缘态。本文中对于该器件处于箱型区域时做了TEM成像,观察到MIT转变后NbOx材料出现了结晶。
器件能够表现出的一些性能
研究人员对整个忆阻器做了一些电学的研究和统计。首先是NDR和器件一些其他电学的性能以及神经元性能的统计研究。下图是这部分研究的结果。

按照表现出的性能不同,研究人员总共把这些行为分成了四种(无NDR、NDR、静态Mott和动态Mott)。根据作者的说法,NDR现象是局部有源(local activity)的特征之一。局部有源这一性能表明一个系统有能力将外部的小扰动进行放大,可以实现放大功能。(其依据是Leon Chua的local activity principle一书)在蔡少棠(Leon Chua)的这本书中,局部有源的定义如下(其原文介绍是基于反应扩散方程的):
.png)
简单来看就是某时刻该元胞会出现能量的净流出,呈现出一个能量源的特性。根据Leon Chua的局部有源理论,可以在参数空间(以二维为例)分出两个区域,一个为无源(passivity)区,一个为局部有源(local activity)区,两个区域相连,但不相交,且连续(disjointed and contiguous)。其中local active区内一个子集称为edge of chaos区域,可以认为处于能量即将瞬时放大的状态。Edge of chaos内还存在一个子集为sharp edge of chaos,较一般的edge of chaos还具有一定的不稳定性。本文的作者们将自身的统计研究结果和Leon Chua的局部有源理论的结果进行了对比,发现理论的说法和实际的实验数据能够得到较好的对应。其中,神经动力学即Mott dynamics对应的区域能够和sharp edge of chaos得到很好的对应,其余的对应关系有static Mott-edge of chaos、NDR-local activity、no NDR-passivity。借助这一理论,本文作者称他们能够加入更多的电物理处理过程,调整化学计量比,从而实现对参数空间内更多的点进行考察,发现了更多的神经元行为。
问题:chua的local activity理论还没完全看懂,欢迎感兴趣或有了解的读者与笔者多交流。
对于整个element而言,作者们做了许多的电学性能测试,在这里做介绍。
不同外部电压下的i-v行为

研究人员们通过对所得的element外接其他的电容和电阻放慢了整个器件的动力学过程,并通过改变外部电压,在一次试验中连续地测试了“新的更大的”element的电学性能。结果见下图(不同的外部电压可刺激element产生不同的电学性能)。
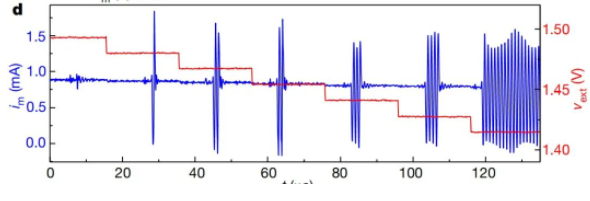
此外,在本文的SI中,作者们还记录了该器件观察到的其他神经元性能。部分介绍如下:
拍中的混沌(chaos in beats):此部分的数据是在器件的动作电位之下进行采集的,电路中包含内电阻,不包含外部电学器件,采用加载外部电压的方式进行性能的测量。做I-t图(电流对时间),可见这时的电性能表现出的是一种有拍现象的振荡。对频率进行分析,可见两个明显的频率峰。外加电压的变化会导致峰位的移动,外加电压的上升会使两峰靠近并穿过彼此。在两峰会聚时,频率峰重叠,振荡的波包变得对外界扰动极其敏感,从而表现出高度不规则性。振荡的poincare图表明,当两峰会聚时,振荡的极限环消失,表明存在混沌。

自持振荡(self-sustained oscillation)、周期脉冲(periodic spike)、周期爆发(periodic burst)和爆发数适应性(burst-number adaptation)的混合。随着外加偏压的上升,会发生不同的行为之间的光滑转变,在某个中间值的偏压下可以观察到多种不同行为的混合情况。
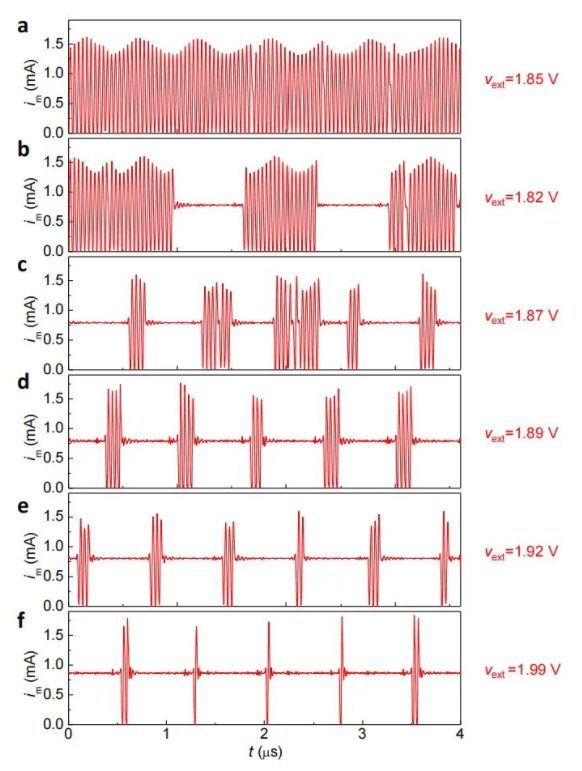
随机发射:混合模式的特例。在对特定的外部电压值响应时,单个的spike会和受抑制的的spike共存,结果就是时间上单个的spike的出现体现出了随机性(整体算上受抑制的spike还是有周期性的),不出现单个spike的地方事实上是被damped spike代替了。

单次脉冲/爆发(或相位脉冲/爆发phasic spike/burst):phasic spike指的是在某个外加电压下,element本身产生一次单个脉冲/爆发,之后就不再产生任何脉冲或者爆发(no spike or burst)。是Izhikevich归纳的神经元行为之二。(图中黑色箭头所对应脉冲是器件刚通电的典型capacitive overshoot现象)
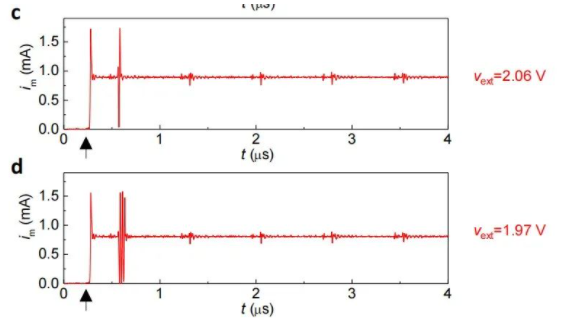
其余的现象详细可见原文SI部分。
数学模型
基于前面得到的转变机理和观察到的一些电学特性,研究人员给出了一个数学模型,可以表现出一些神经元的性能,模型如下:
对于本模型的解释:其中,式3、4可以通过基尔霍夫定律,根据电路图很容易能够推导出来。对于式1,采用的是肖特基发射的公式,原文作者认为,任何非线性的热输运都可以导致NDR。笔者认为,相比于他们之前所发现的NDR-1区域的Poole-Frenkel机制,肖特基热发射的式子形式类似,且更为简单,所以原文作者可能基于此采用的本式,他们也提到了这一模型并不是对实验结果模拟的最精确的模型。对于式2,描述的是器件本身的发热-散热过程,发热项描述的是发热功率除以热容得到的是器件整体的温度上升速率;散热项描述的是温差和热阻及热容的商是温度的下降速率,由牛顿冷却定律可推出,两者合起来是温度的整体变化速率。式5则是原文作者们描述的Mott转变过程,采用了符号函数表征电阻突变的过程,此外后面提到参数beta等于1,从而使得Rmet数值可以在0~2R0之间变化(作者在后续提到该条方程也未必非常准确,比如I1和I2的数值未必准确)。这里对于忆阻器的建模采用了一种等效的方法,将单个的忆阻器转换成了Rsch(其i-v特性用Isch表征)和Rmet的并联。
.png)
用这个模型所得到的仿真结果是:
注意,此处的四个不同的神经元行为类似于实际器件的但不完全一样,设定的4个外部电压和实际用的外部电压之间的数量上的不同。此外,仿真1.7V下表现出了非常一致的振荡行为,而不是实际器件那样的有一些不稳定性的行为。并且原文作者在左侧的i-v图中没有标出chaos、beats等行为,不知是否是因为该模型暂时还无法体现出这些行为,又或者如他们所说,实际观察到的chaos可能体现了包括外部扰动,仪器共振等的影响。不过另一方面,后三者所描绘的periodic burst/spike以及damped spike现象又属于神经元的特性,在这方面也可以说这个模型在模拟神经元的道路上获得了一定的成功。(此模型不是为了完整的描述生物神经元的行为,而是期望能够将实际的element的神经元性能通过仿真表现出来)
仿真得到的结果可以对应实际生物神经元的几个过程:(见下图)
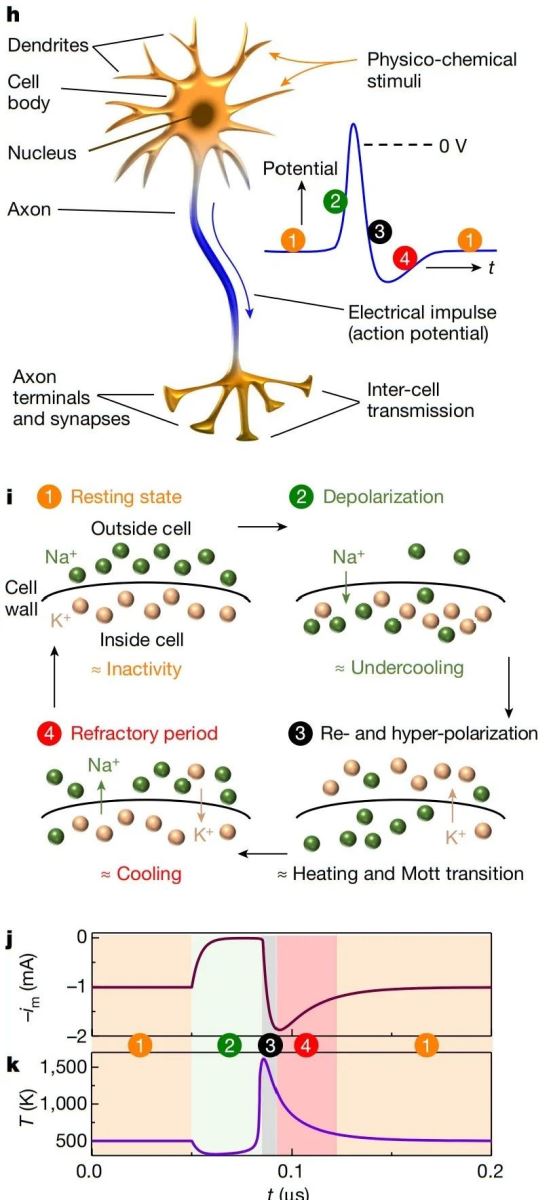
图h描述的是实际生物神经元的动作电位过程,其电位最高值对应的是刚刚超过0V,大多数时候电位都在0以下。生物的神经元产生动作电位到恢复总共4个过程,分别为静息电位-去极化-复极化-不应期。对应于该element过程分别是不活动(inactivity)-过冷(undercooling)-加热及发生Mott转变和冷却过程。注意仿真时得到的电流均为正值,原文作者们将其做了简单反相(-im),得到的电流中spike的仿真结果能够对应上真实的生物神经元的动作电位的四个阶段(图j)。其相应的温度变化见图k。能够对应上过冷时低于500K和发生Mott转变时达到1000K以上,符合假设和之前的实验结论。
三阶意味着复杂性
原文非常重要的一点是构造了一个三阶的子电路,无论是从实际器件还是构建的数学模型上。实际器件上,这一器件,无论是从原文作者团队自身,还是其他研究团队来看,之前也做过许多类似结构的器件,但是在原文中这一element表现复杂的神经元性能的潜能才算是首次报道出来。作者团队是这样解释的:他们的分析表明对器件的设计和制造要十分仔细,使得器件拥有合适的电、热、化学性能,从而能够支撑神经元性能的实现。这是什么意思?
作者提出,一个动态电路元件的阶数是其相空间的维数,也即系统接电时,能够随时间发生变化的状态变量(state variable)的数目。状态变量代表着在任意时刻能够影响器件导电能力的不同性能。大多数器件都可以至少具有一条微分方程,或者说有着一阶的复杂性,一般会是温度作为一个状态变量。但是实际的应用过程中一般不会关注温度的变化(可能是温度的变化导致的影响不算很明显),导致温度相关的动力学常被忽略。这造成的结果就是系统的复杂性经常被降一阶,比如说低功率下工作电阻就会被降到0阶。对于一般的非线性元件的数学建模,每一条描述一个状态变量的时域变化的状态方程就会是一条时域内的一阶常微分方程,从而提供了一阶的复杂性。因而,状态变量的数目决定了状态方程的数目,进而决定了体系的复杂性。
如何说明三阶产生复杂性,作者举了两个例子。第一个为一个二阶系统的仿真。(注意模型的不同)此处作者不采用并联Rmet的方式来表示Mott转变,而是采用类似其在2017年发表的文章中的模型来描述Mott转变(doi:10.1038/nature23307)(笔者的理解,不一定准确)。其在2017年发表的文章中,将Mott转变的结果归为热阻(Rth)值的突变。相比于原文正文中的数学模型,作者去掉了Rmet项来表示Mott转变,并且将Rth表示成一个温度T的光滑函数(不是2017年文章那样的突变,但使用了激活函数形式,十分类似)。由于如此操作少了一条ODE,因而复杂性降低一阶至二阶。对这样的模型作者进行了仿真。结果如下:
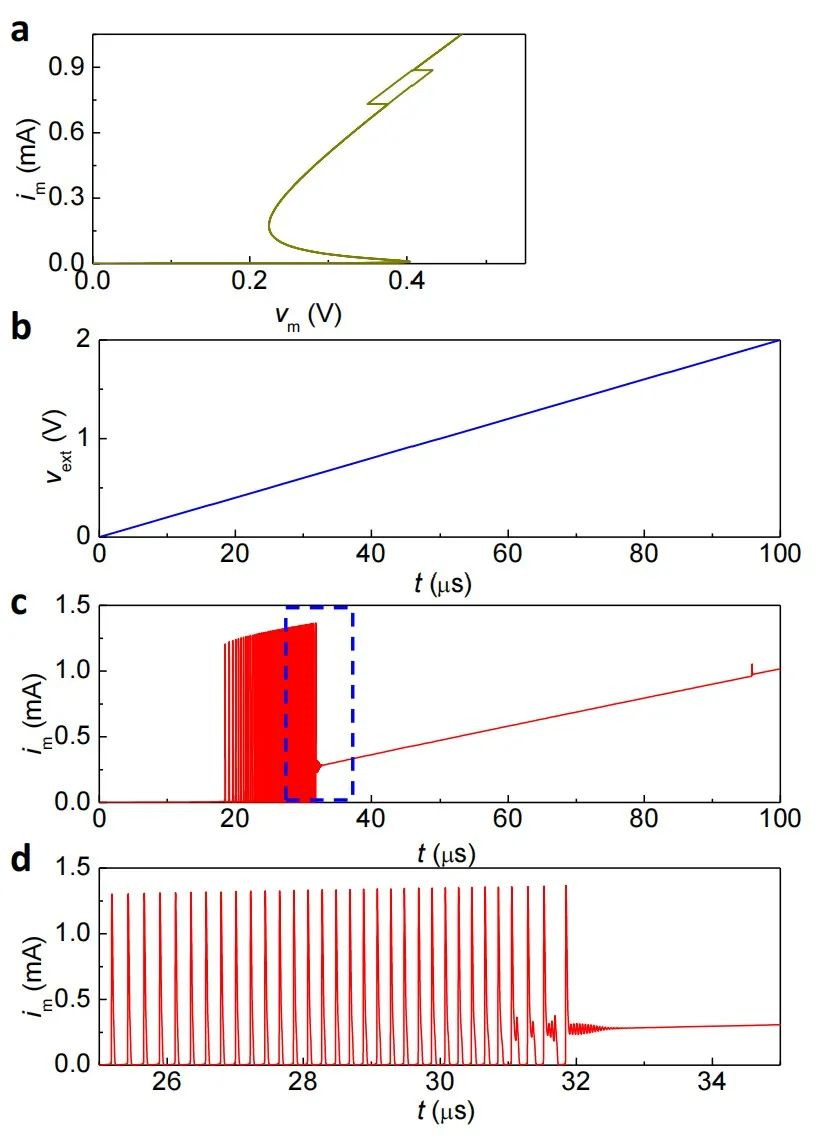
这样的模型虽然随着外部电压的变化能够表现出一些震荡性能,但是关键的神经元特性(比如periodic burst和periodic spike)却不能产生。这暗示了这些神经元性能可能需要更高阶的复杂性。
第二例是改变一条方程的形式,但是仍然使其包含微分项。作者将正文原模型式5换为:
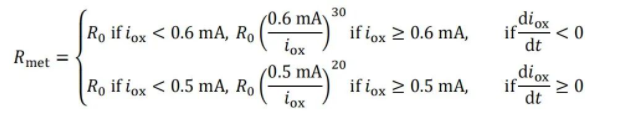
如此一来模型不同,但是仍然保证了三阶的属性。得到的仿真结果如下图所示:
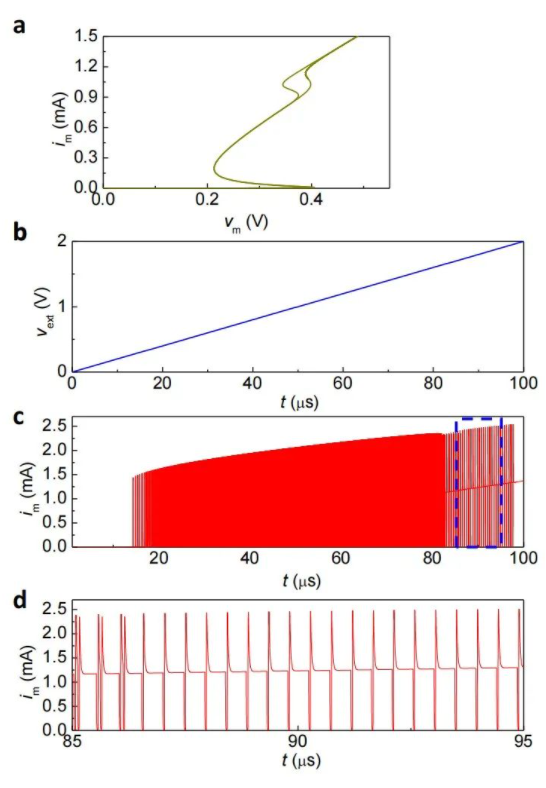
作者提到,也可以换用其他不同的数学形式来表示,只要维持三阶,仍然能够表现出periodic burst等神经元特性。
与传统计算的对比
这一新兴element在应对传统MOS基计算具有一些自身独特的优点,除了文章开始提到的低功耗等,作者还展现了两个有着其他方向竞争力的实例。
第一个是在布尔运算中的潜力。该例子说明较为简单。该器件的简单集成搭配上一个可调节的耦合电阻可以实现运算逻辑的可调。结果如下:
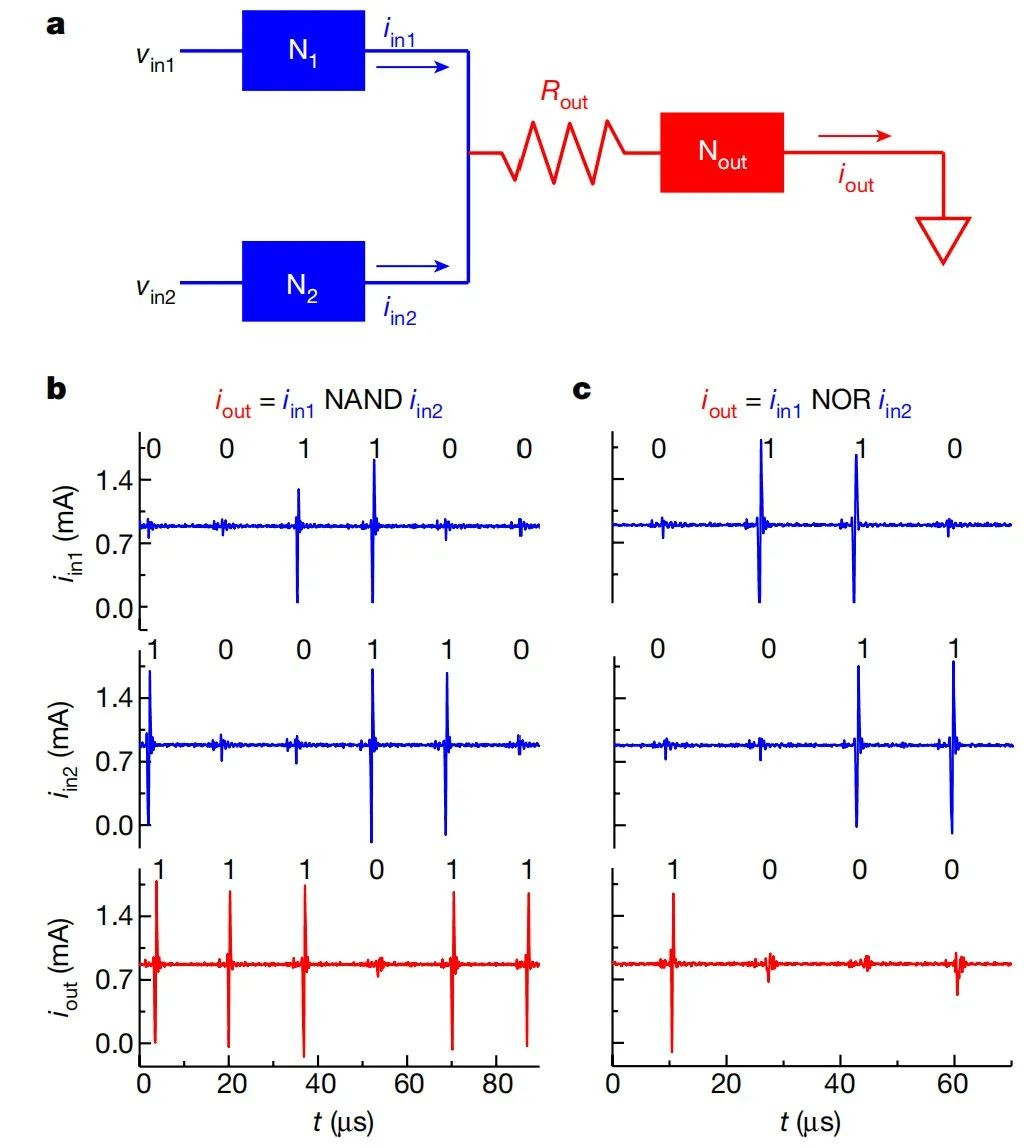
图b和c展现的是两种不同的运算逻辑,而它们之间的转化只需要调整Rout的数值即可实现。
病毒准种重建问题-图分割问题
(此小节中振荡器或神经元一般指的就是前面的element)
首先介绍这一部分中用到的另一新器件——伪忆容器。在华中科大缪向水教授的《忆阻器导论》一书中,本文所称伪忆容器(pseudo-memcapacitor)没有伪字,缪教授所著书中将这种器件直接称忆容器。本文所用的伪忆容器是通过组合电容和忆阻器实现忆容功能的,在这里的忆阻器的特性是非易失性的两阻态忆阻器。电路结构如下:
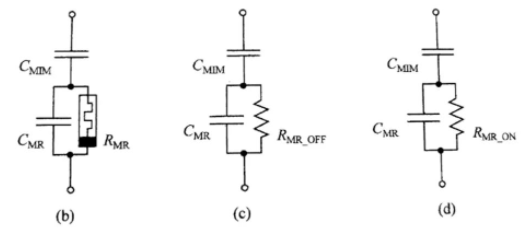
当忆阻器处于低阻态时,阻值小,近似短路并联的电容,造成电容值大(阻抗呈现为容性)。当忆阻器处于高阻态时,近似断路,造成等效两电容串联的效果,总电容值小(阻抗会呈现为阻性)。因而只要通过对忆阻器的操作,就能够实现对伪忆容器的设置(如下图所示)。
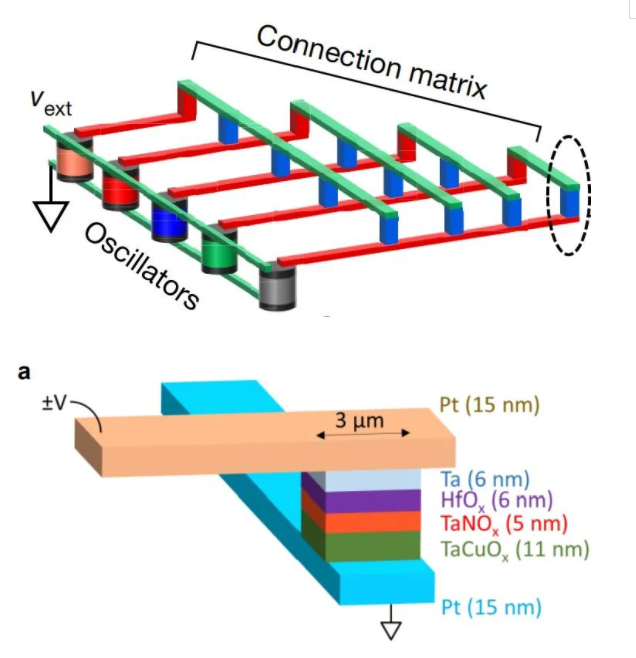
这部分另外一个重要的原理是基频相近的振荡器(即前面的element)之间耦合后的行为。耦合后的振荡器之间在稳定之后,其振荡的相位往往有着明显的相互影响关系。当两个振荡器之间是阻性耦合(即两个振荡器用电阻连接)时,它们最终会达到相同相位的同步(或者接近同步)。当两个振荡器之间是容性耦合(两者的连接线中接入一个电容),它们最终会达到反相的“同步”。因而,当一个振子耦合体系最终稳定时,我们可以按照不同的相位将振子们分为至少两类并编号(本例中是两类),比如说某一相为“+1”,与之相反的为“-1”。如果说要考察一个多个振子之间相互影响的实例,可以设计出一个大的连接阵列,阵列上每个“点”都是不同的电学元件(电容或者电阻),再将基频相近的振荡器连上阵列,构成了一个振荡器之间相互连接的网络(如下图所示)。

当然,本实例中上图所示的连接矩阵(connection matrix)的每一个点事实上都是由伪忆容器构成的,其阻抗属性的调整通过预先的对伪忆容器中的忆阻器进行编程而实现。此外,实例中首先是制作了一个N×N的阵列,由于振荡器之间的连接是双向的,因而用矩阵来表示振荡器之间的连接情况的话连接矩阵会是一个对称的矩阵,因而实际应用中只需要一半的矩阵就能够表示振荡器之间的连接,所以在制备得到连接矩阵之后,右上角的一半的点阵没有经过forming处理,其阻值极大(~1GΩ),对角线上的点全部硬击穿或者短路,以实现对角线最终数值为0;左下角的一半经过forming处理之后,进行编程,从而实现一个振荡器之间连接网络的制作。
当矩阵编程完成,振荡器接上连接矩阵并通电起振后,不同振荡器之间会发生什么相互影响?按照前面的叙述,阻性连接的振荡器之间会趋向于同相,而容性连接的振荡器之间会趋向于反相。
但是,同时受到多个其他的振荡器的影响时,一个振荡器的相位又该如何决定?作者指出,在整个体系开始工作时,体系会经历一个各振荡器(或者说神经元)之间相互影响而整体会不断趋向于稳定态的过程,这样的一个稳定态本质上是一个能量最小的点。因而,整个体系会执行一个能量最小或者成本函数最小化的过程。作者表示这类似于Ising模型或者Hopfield网络。作者尤其提到,这样一个连接网络搭配振荡器的系统尤其适合于优化问题,而在应用的场景中连接矩阵的设置(各点的状态)就是输入的问题,当给振荡器通上电时,体系自身就开始执行优化过程,并在稳定态时给出最优解。另外,作者提到,这样一个耦合振子体系和大脑皮层的计算过程有很多的相似之处。
作者在演示忆阻器用于模拟计算(analogue computing)的潜力时,举了病毒准种重建的例子,并称病毒准种重建问题可以转化为一个图分割问题(此外还可以用Markov模型、probabilistic mixture model等解决),问题的核心目标就是将冲突图分割成两个或多个子集(分割出的子集数量视设定的参数的状态数目而定)。作者提出可以用这样一个能量函数来表征冲突图体系的能量:

其中,sij是(i,j)处的邻接矩阵的元素值,ai是第i个点的读数(共+1和-1两种读数)。Sij的标记是:1代表ij两点存在冲突,0代表没有。用这样一个能量函数,在对其最小化之后,可以将整个冲突图分成两个子集,集内的冲突值最小。而前面的耦合振子系统也能执行类似的任务。耦合振子系统的能量函数,按照Ising模型,写成这样:
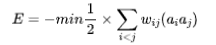
对比图分割的能量函数,两者相似,可以将w理解成-s。而w指的是连接矩阵中的各权重(即容值的大小,因为容值在分割过程中更为重要)。W的数值而言,可令冲突连接对应于-1或者其他的能够促使图发生分割的数值。由此构建了图分割问题邻接矩阵到耦合振子系统连接矩阵权重的一个映射(mapping)。
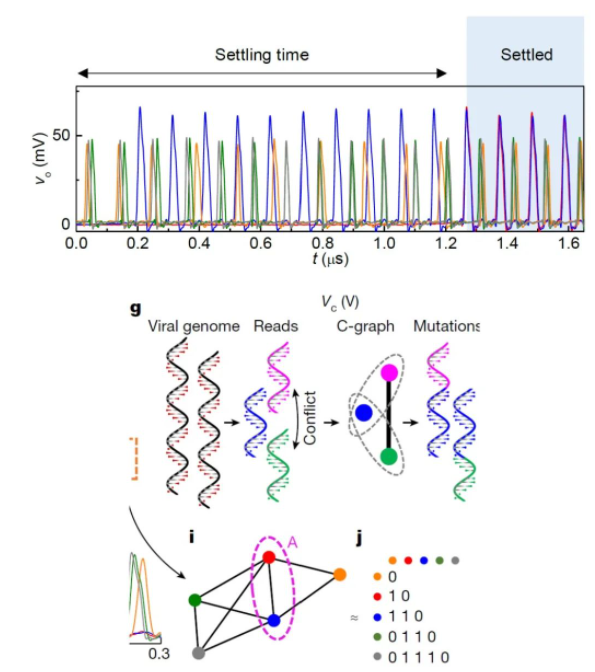
作者指出,由于本例只是一个演示,因而没有特别专门的设计权重矩阵,并且一个随机编程的矩阵也能够表示更多的实际问题,因而实例中的矩阵为一个随机的矩阵(就是他们对伪忆容中的忆阻器的操作实际上相当随机、写意,并没有专门设计一个矩阵)。实例中,高容值(high capacitance)的连接代表了-1的权重,而低容值代表了0的权重。在编程结束后,将所有的振荡器连接在连接矩阵上,并通上同一个外电源,用示波器观察各个振荡器的振荡相位变化。各振荡器会经历一个稳定过程,稳定后可以观察各振荡器的相位,了解到最终哪些振荡器形成同相振荡,它们与剩余的另外一部分形成了反相同步。
用这样的方法执行的优化过程,具有速度快(N=16时,用20个脉冲,共耗时2us完成优化),能耗低(单个脉冲20pJ)的优点。这两点,尤其在这个问题(该问题为一个NP-hard,nondeterministic polynomial-time-hard,传统计算机计算相对低效)上,体现出了对传统计算机优势。并且在连接数更大的时候,体现出对电子计算和量子计算的更大的优势。作者提出,这项实验可以作为检验计算能效性能的一项指标实验,鉴于当前大多数计算包括量子计算在内都属于高能耗的,而用于检验计算能效的标准比较少。他的能够促使图发生分割的数值。由此构建了图分割问题邻接矩阵到耦合振子系统连接矩阵权重的一个映射(mapping)。作者指出,由于本例只是一个演示,因而没有特别专门的设计权重矩阵,并且一个随机编程的矩阵也能够表示更多的实际问题,因而实例中的矩阵为一个随机的矩阵(就是他们对伪忆容中的忆阻器的操作实际上相当随机、写意,并没有专门设计一个矩阵)。实例中,高容值(high capacitance)的连接代表了-1的权重,而低容值代表了0的权重。在编程结束后,将所有的振荡器连接在连接矩阵上,并通上同一个外电源,用示波器观察各个振荡器的振荡相位变化。各振荡器会经历一个稳定过程,稳定后可以观察各振荡器的相位,了解到最终哪些振荡器形成同相振荡,它们与剩余的另外一部分形成了反相同步。
用这样的方法执行的优化过程,具有速度快(N=16时,用20个脉冲,共耗时2us完成优化),能耗低(单个脉冲20pJ)的优点。这两点,尤其在这个问题(该问题为一个NP-hard,nondeterministic polynomial-time-hard,传统计算机计算相对低效)上,体现出了对传统计算机优势。并且在连接数更大的时候,体现出对电子计算和量子计算的更大的优势。作者提出,这项实验可以作为检验计算能效性能的一项指标实验,鉴于当前大多数计算包括量子计算在内都属于高能耗的,而用于检验计算能效的标准比较少。
文:张泽锋
注意:文中作者一词单指原文作者或其团队,笔者仅为该篇稿件作者。


 loading......
loading......