传统的人工神经网络由于其出色的非线性表示能力, 已经在诸如图像分类等各种任务上取得了成功的应用, 但是前向的神经网络结构也限制了其处理时序相关问题的能力, 为了使神经网络具有某种时间记忆性, 循环神经网络(Recurrent Neural Network, RNN)应运而生, 其通过引入隐层之间的循环连接结构达到短时记忆的效果, 但是更复杂的连接结构也使得训练变得更加困难, 需要大量的计算, 占用大量的内存. 在本世纪初, 两个研究小组独立提出了一种与人类小脑处理信息的结构极其类似的脑启发式算法, 如图1所示.  Jaeger在2001年提出了回声状态网络(Echo State Networks, ESNs)[1], Maass于2002年提出流体状态机(Liquid State Machines, LSMs)[2], 最终Verstraeten等人以实验证明这两种网络本质上是一样的, 并将其统称为储备池计算(Reservoir Computing, RC)[3]. RC可以看作一个扩展的三层循环神经网络(输入层、隐藏层和输出层), 这种循环神经网络利用随机初始化的连接, 将低维输入映射到高维状态空间, 并在高维状态空间中保持动力学信息. 与传统的神经网络不同, RC网络中从输入层到隐藏层的连接权重和隐藏层内的循环连接权重随机产生且不需要进行训练, 只有输出层的参数被训练用来根据输入序列在隐藏层中的表示来区分输入序列. 通过只训练无记忆输出层, RC网络的训练成本比SOTA网络要低得多。

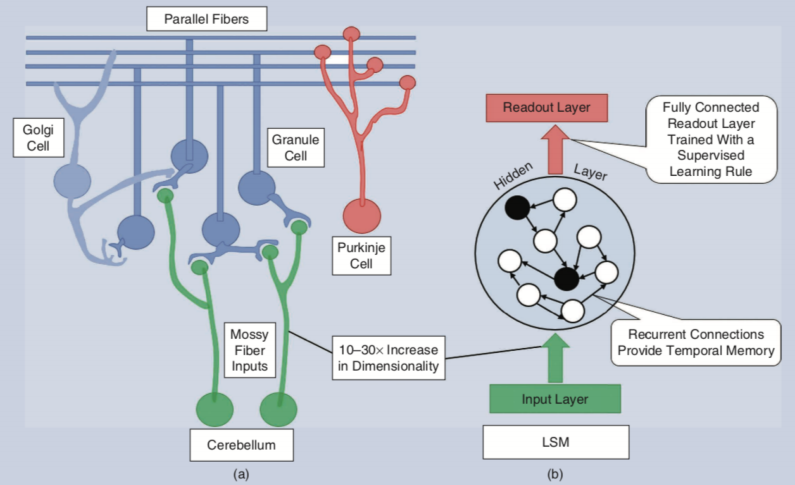
图1:(a)人类小脑处理信息的相关结构. (b)流体状态机模型结构. 图片引自[4].

1.数学模型及训练

1.1数学模型

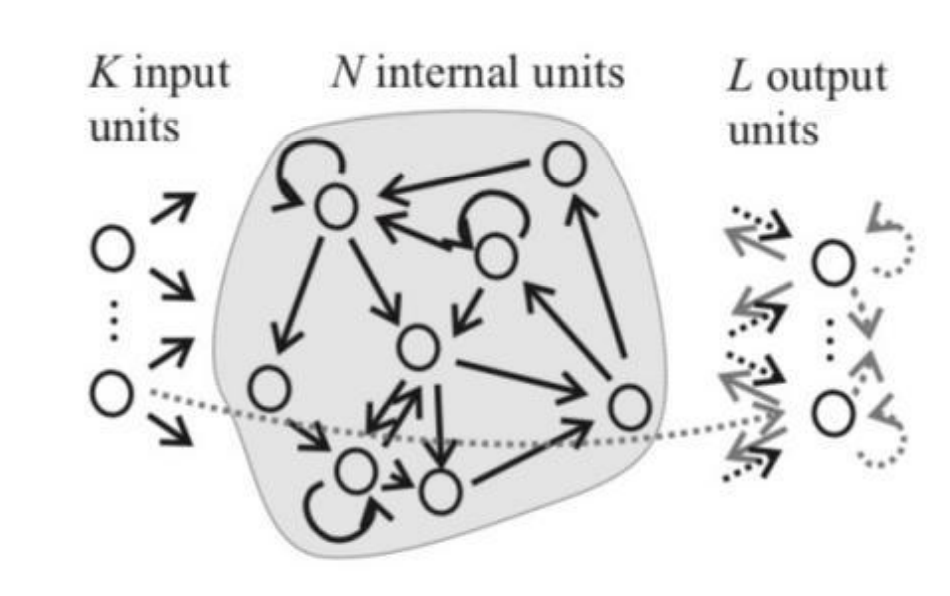
图2: RC 网络结构.

      一个传统的RC网络结构如图2所示, 其由三部分组成, 一个由个输入神经元组成的输入层, 一个随机可循环连接的具有个中间神经元的隐藏层(reservoir), 以及一个由个输出神经元组成的输出层. 其中, 输入神经元随机稀疏地连接到隐藏层的中间神经元, 其连接权重矩阵记为，隐藏层内部的神经元以一定的规则稀疏连接，其连接权重矩阵记为，中间神经元与输出神经元之间全连接，其连接矩阵记为. 有些RC网络还允许从一些输入神经元直接连接到输出神经元, 其对应的矩阵记为, 以及从一些输出神经元连接到另外一些输出神经元, 其对应的矩阵记为, 甚至有些RC网络还允许从输出神经元反馈回中间的隐层神经元, 将其对应的矩阵记为. 此外, 记时刻的个输入神经元, 个中间神经元, 以及个输出神经元对应的状态量分别为：

      则根据时刻的输入值, 中间状态量以及输出值, 可以得到时刻的状态和输出方程：

       这里表示中间隐层神经元采用的非线性激活函数, 表示输出神经元采用的激活函数, 一般为线性激活. 在上述权值矩阵当中, 连接到中间隐层神经元的权重都是服从随机分布(正态分布、均匀分布等)初始化且保持不变, 只有连接到输出神经元的权值是通过训练得到。

1.2神经元类型

      在RC中, 神经元类型的选择同样会大大影响网络的性能. 当前主流的RC网络一般采用以下几种神经元: 线性神经元(恒等映射), 阈值逻辑神经元, 型神经元(sigmoid，tanh), 脉冲神经元. 对于脉冲神经元, 一般采用Leaky-integrate-and-fire(LIF)模型来描述神经元的动力学. 一般地, 输入层是线性神经元, 输出层会选用线性神经元或型神经元, 对于中间隐层神经元, 传统的ESN采用型模拟神经元, 而LSM则采用脉冲神经元。

1.3模型训练

      根据训练集提供的时序数据以及RC的实际输出值, 利用均方误差作为损失函数. 这里我们假设所有的输出神经元只与中间隐层神经元相连. 在输出神经元为线性的情形下, 这相当于求解矩阵的逆. 更一般地, 如果权值矩阵为非奇异阵, 可以通过求解其Moore-Penrose伪逆来得到最优的中间隐层神经元到输出神经元的权值矩阵[5]. 因此, 整个训练过程可以视为一个简单的线性规划问题, 由此不难看出RC的训练成本相较于其他处理时序问题的RNN大大减少.

2.RC重要参数和指标

      在搭建RC网络结构时, 需要考虑如下两个结构参数:

1.储备池规模

      直观上, 储备池的规模应该视具体任务来决定, 任务的复杂程度越高, 需要的储备池规模越大, 来实现足够长的时间记忆能力以及产生足够高的维数表示, 使得输入数据可分. 随着隐藏层的增大, 输入数据被映射到更高维的空间, 其可分性随之提高, 受网络初始化的影响也会更小, 但不可避免的也会出现过拟合的现象, 因此需要选取合适的储备池规模. 基于输入维数大小, Kumar等人提出, 隐藏层的规模应为输入空间的10-50倍[6]. Lukosevicius则提出隐藏层的维度应该等于输入空间的维数乘以需要记忆的时间步数, 也即预测时间序列所需要的时间步数[7]。

2.神经元连接概率

      在RC中, 输入层到中间隐藏层的连接是稀疏的. 有研究表示, 对于维输入, 我们只需要的连接度即可创建一个完整的高维表示. 而对于中间的隐藏层, Maass认为神经元之间的连接一般是基于相邻的神经元更容易连接的原理, 因此定义隐藏层中两个神经元连接的概率为：

      其中衡量两个神经元之间的距离, 参数表示两个神经元连接的最大概率, 可以调控整个隐藏层连接度稀疏程度. 控制距离的变化对连接概率的影响程度。

      在Han等人的实验中可以看出RC的记忆容量(Memory Capacity, MC)与隐藏层连接的稀疏程度之间的关系[8]. 如图3, 当时, MC值随着网络密度的增加而增加, 直到时，MC值基本保持恒定, 之后逐渐下降. 该实验结果也直接证明, 即使隐藏层神经元之间的连接非常稀疏, RC也具有较高的记忆能力。

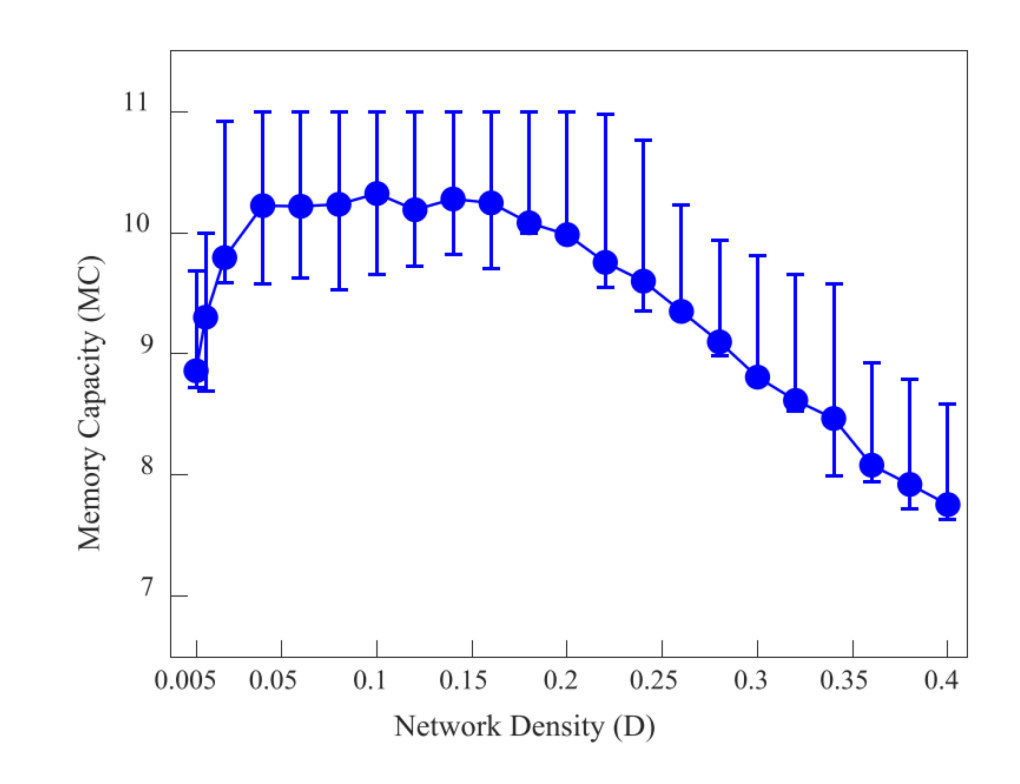
图3: RC 的记忆容量 MC 与隐藏层连接的稀疏程度 D 之间的依赖关系. 图中的点代表 100 次重复实验的平均 MC, 误差条代表 MC 的第 1 个四分位数和第 3 个四分位数. 图片引自[8].

      在搭建好RC之后, 可以通过以下几个指标来衡量RC的性能：

1.Lyapunov指数

      针对时序预测任务, 可以用Lyapunov指数衡量相似的两个输入值对应的隐藏层状态的发散程度, 用于衡量RC的混沌程度\cite{Kudithipudi}[4].

2.分离属性

      针对分类任务, 一般用分离属性来衡量RC性能. 分离属性是指从低维输入映射到隐层的高维表示后是可分离的, 以便输出层的线性分类器可以学习不同类别之间的决策边界. 我们希望不同类别的输入对应的表示是高维线性可分的, 相同类别的输入对应的高维表示是相似的. 基于此, 我们利用隐藏层状态的类内方差与类间方差的比值来定义RC的可分离性, 同时这个值也一定程度上反映了RC的泛化能力[4]。

      其中为类内方差, 为类间方差, 越小表示RC的分离属性越强.

3.塑性参数

      此外, 一系列研究[9-14]还通过引入塑性参数(Intrinsic Plasticity, IP)来反映RC的适应性, 通过优化IP来减小RC的随机化程度, 构建对于具体任务更加优化的特异性的RC网络结构.

3.RC在时序相关问题上的应用

      在很多时序相关问题上, RC已经取代传统的RNN, 展现出巨大的应用前景. 下面介绍两个RC的成功应用实例.

3.1模型未知的大型时空混沌系统预测

      早在2004年, Jaeger和Haas就已经将RC应用于预测低维混沌系统, 并取得了良好的效果[15]. 2018年, Edward等人通过并行计算策略将RC应用于大型时空混沌系统的预测[16]。

      假设系统的动力学模型未知, 但可以获得有关系统状态演化的准确且完整的观测数据. 在这种情况下, 如何有效的预测大型时空混沌系统的未来演化, 一直以来是一个十分困难的问题. Edward等人借助RC网络搭建了一个模型未知的大型时空混沌系统预测系统. 他们以Kuramoto-Sivashinsky方程:

      作为时空混沌系统的预测目标模型, 在预测过程中, 他们注意到随着空间尺度的不断增大, 如果仅仅采用单个RC进行预测, 则其所需的隐藏层规模也要不断增加, 这使得预测难以进行下去. 基于此, Edward等人提出了一种由一系列中等规模的RC组成的并行预测方法, 使得每一个RC只负责预测时空系统的一个小的局部区域. 如图4所示, 在空间维度上将系统等分为个部分, 每个RC负责其中一个空间区域的预测任务, 其输入为对应空间及其左右相邻的部分区域的观测数据。

      最终, 在混沌占据主导之前, 他们在KS方程上达到了八个Lyapunov时间的精确预测, 这大大提高了当前大型时空混沌系统的可预测长度. 这一结果不仅为大型时空混沌系统的无模型预测提供了一种有效的潜在手段, 也在实验上印证了RC处理时序问题的出色性能。

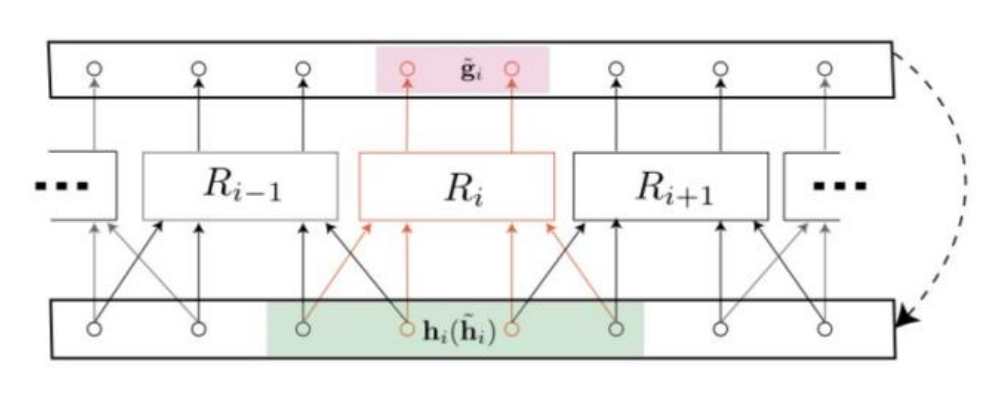行 RC 方法处理大型时空混沌系统预测示意图. 展示了其中一个 RC 的运行过程, 粉色区域表示该 RC 在空间尺度上的预测范围, 绿色区域表示该 RC 在空间尺度上接收的输入信息范围, 右侧虚线表示在自主预测阶段的反馈连接.

3.2时间序列不稳定周期轨道的检测

      Zhu等人创造性地将RC与自适应延迟反馈控制结合起来, 用来检测非线性动力系统中的不稳定周期轨道(Unstable Periodic Orbits, UPOs). 他们同样聚焦于模型未知, 而仅仅知道时间序列的观测数据的情形, 来检测和提取UPOs[17]. 具体而言, RC框架用于恢复动力系统对应的向量场, 随后采用自适应延迟反馈控制(Adaptive Delayed Feedback Control, ADFC)[18-20]对恢复的系统进行UPOs的检测. 利用RC估计向量场方法如下所述。

     对于一个常微分方程组定义的非线性动力系统：

      利用RC框架和训练数据可以得到该动力系统在离散时间上的估计

      这里我们记为RC的输入以及目标输出, 为中间状态. 令, 可以得到

      因此可以将看作原动力系统向量场的一个很好的近似, 这样, 对于一个模型未知而只有观测数据的动力系统, 根据RC得到了其对应的向量场, 再利用ADFC技术即可通过已有的模型未知的观测数据定位嵌入在混沌系统奇异吸引子中的UPOs。

4.针对RC的理论分析和理解

4.1稳定性分析

      Jaeger在提出ESN的同时给出了该网络稳定的一般充分性条件, 他首先定义了网络的回声状态属性[1]。

      定义1+——(中文版本引自[21]） 未训练网络具有连接权重矩阵, 网络的输入样本数据和输出样本数据分别来自紧集和, 称网络关于紧集和具备回声状态属性, 如果对每一个输入/输出序列和所有的状态序列满足：如果

      则, 对于所有的成立。

      通过以上定义，不难看出回声状态属性的意义, 即如果网络已经运行足够长的时间, 网络的中间隐层状态只由当前的输入输出决定. 随后, Jaeger在理论上证明了在RC没有反馈连接的前提下, 保证隐藏层内部神经元的连接权值矩阵的谱半径小于1, 即可使隐藏层具有上述回声状态属性, 进而确保网络具有渐进稳定性[1]. 但这只是一个相当宽泛的充分条件, 在此基础上, Buehner等人提出了一个更为严格的网络稳定性条件, 以保证RC网络的渐进稳定性[22]。

4.2从同步化角度对RC有效性分析

      Zhu等人在将RC与延迟反馈控制结合进行时间序列不稳定周期轨道的检测过程中受到启发, 提出一种同步化的观点用于分析RC的作用[17]. 考虑目标时间序列为一个一般的非线性动力系统, 其由一个常微分方程组描述:

将其近似地写成离散形式：

      在RC网络中, 用代替输入, 可以得到：

      因此, 利用训练集中的时间序列成功训练RC网络, 相当于实现与之间的同步, 为了达到这种同步, 在RC的原始输出上加上一个耦合项, 得到如下形式：

      以上三式构成一个离散时间的动力系统, 进一步可以计算与的误差满足的动力学方程：

      记为第一项中矩阵最大特征值的范数，并记为第二项中误差对应的范数，为了实现上述同步，同时满足误差动力系统的渐进稳定，至少需要满足以下两个条件：

      对于某个常数以及足够大的成立。

4.3储层结构的性质对RC短时记忆的影响

      短时记忆特性是RC的一个基本动力学特性, Jaeger引入了记忆容量(Memory Capacity, MC)这一指标来量化RC这种短时记忆的特性[1]. -delay MC(记做)度量了RC在输入下复现出其延迟版本的性能, 其定义为：

      可以将其视为目标输出与RC真实输出之间的相关系数, 相关系数越大, 说明复现结果越好, 进一步意味着RC对时间前的信息记忆能力更好. 进一步, 将全局MC记为：

      一方面, 对每一个, 如果RC可以重建, 则其对应一个输出层的权值矩阵

      根据上式不难得到：

      另一方面, 假设隐藏层对应的是一个有向无环图(Directed Acyclic Network, DAN), 其最长路径为P, 则任意两个隐藏层状态初值对应如下关系:
由最长路径为P易知

      因此隐藏层状态仅仅显式依赖于之前P-1个时间步长的状态, 这说明其最大记忆时长在理论上被P-1限制. 随后, Han等人还通过数值实验验证了这一理论分析, 同时发现, 随着储备池规模的增加, 记忆能力先是随隐藏层最长路径的增长而线性增长, 但规模过大后其增长趋势逐渐放缓, 这一定程度上说明了隐藏层规模的增大不能无限制的增强RC的记忆能力[8]。

5.RC拓扑结构优化

      从上述理论分析可知, 单纯的增大隐藏层的规模并不能无限制的增大RC的时间记忆能力, 其浅层架构本身限制了RC无法实现长时间的记忆. 在这一部分, 我们介绍当前针对RC拓扑结构优化的最新研究成果, 这些成果一定程度上都提高了RC的时序预测的尺度或精度。

5.1深度储备池计算

      由于RC是一个浅层网络结构, 其记忆能力大大受限, 因而很难处理长时间尺度的信息. 为了增强其时间记忆能力, Soures提出一种名为Deep-LSM的深度RC网络结构[23]。

      如图5所示, 在深度RC网络中, 增加了中间隐藏层的个数, 隐藏层之间采用一个赢者通吃编码器(Winner Take All, WTA)对从上一隐藏层输出的高维表示提取其低维特征, 在将提取到的低维特征输入到下一个隐藏层中. 起始隐藏层状态由输入层和上一时刻该隐藏层状态决定, 之后的每个隐藏层由上一隐藏层状态经过WTA层得到的低维表示与上一时刻该隐藏层的状态决定. 最后一层是一个注意力调整输出层, 用于关注每个隐藏层中特定的重要的信息, 它计算每个隐藏层, 以及单个隐藏层中每个神经元的注意力系数, 再根据这些系数对各个隐藏层状态进行加权求和, 最终得到输出. 该深度RC网络在语音识别等方面均优于传统RC。

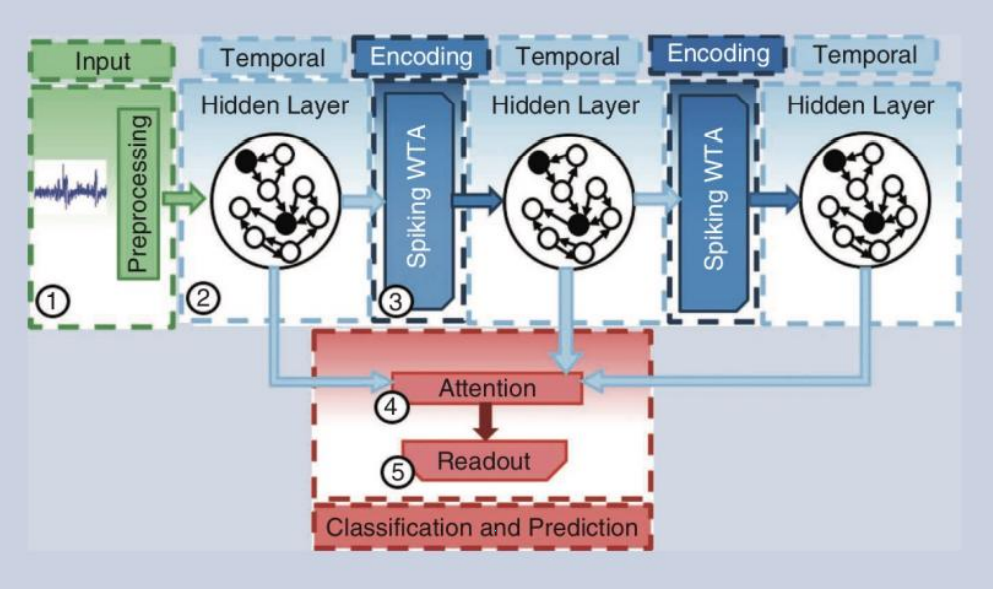
图5: Deep-LSM 结构示意图. 图片引自[4].

5.2聚类储备池计算

      Han等人通过分析RC模型的短期记忆特性来试图解释其内在的动力学特性, 这种特性可以通过全局指标MC来量化. 他们研究了隐藏层为DAN的RC的全局MC, 发现其全局MC在理论上以隐藏层对应的DAN的最长路径的长度为界, 并基于此提出了聚类RC模型[8]。

      由于RC的MC与隐藏层的结构密切相关, 所以具有相似空间结构的中间隐藏神经元应该具有相近的记忆容量. 因此, 在聚类RC中, 首先利用改进的struc2vec算法[24]捕捉节点的结构相似度, 根据其定义的神经元之间的结构距离得到了层次带权图, 如图6, 并根据层次带权图将RC的隐藏层神经元聚类划分为几个记忆社区结构, 使得每个社区中的神经元具有相近的记忆容量. 在训练阶段, 每个记忆社区内的状态到输入层的权值矩阵是独立训练的, 由此生成一些中间输出量, 再将这些中间输出进行平均得到最后的输出。

      Han等人通过实验验证了这种聚类RC在对于Lorenz混沌系统和Rössler混沌系统的预测性能方面均优于传统RC, 并且聚类RC的训练成本也一定程度上低于传统RC。

图6: 根据原始 RC 中隐藏层对应的有向无环图生成层次带权图示意图. 图片引自[8].

 

6.RC对深度学习的启发性应用

      由上述介绍可以看出, RC的隐藏层连接具有很大程度的随机性, 但这种随机性非但没有影响其处理时序问题的能力, 反而使其可以很好地泛化应用于各式各样的问题. 这种随机的思想对其他深度学习架构也起到了一定的启发性影响. 研究人员发现, 在某些神经网络中适当加入随机性的结构, 非但不会影响其表现性能, 反而在提高训练效率的同时增加了神经网络的泛化能力。

      本文以Transformer这种新型网络架构为例, 介绍应用RC随机性思想提升深度学习模型性能的最新研究进展. Transformer是Vaswani等人在2017年提出的一种模型架构[25], 其颠覆了传统的利用RNN进行序列建模的思路, 只利用encoder-decoder和attention机制就全面击败了SOTA, 并且由于其具有可以并行计算的优势, 目前已经广泛应用于自然语言处理的各个领域。

在2021年, Shen等人受到RC随机性思想的启发, 提出一种Reservoir transformers的新型transformer架构[26]. 其主要思想是通过冻结一些层, 使其参数在随机初始化之后保持不更新的状态, 来权衡计算复杂度和网络的表现性能之间关系. 他们发现, 最先进的transformer架构可以在不更新一些层的参数的情况下进行训练, 并且在诸如机器翻译等任务中, Reservoir transformer在其引入的AUCC度量下实现了更好的性能-效率之间的权衡, 训练时间缩短, 收敛速度变快, 并且在测试集上展现出更优秀的泛化能力。

      Choromanski等人同样受到这种随机化的思想的启发, 提出一种名为Performer的具有注意力线性扩展机制的新型transformer架构[27], 它依靠一种FAVOR+(Fast Attention Via positive Orthogonal Random feature)机制随机近似softmax attention kernel, 提供了可扩展, 低方差, 无偏估计的注意力机制, 可以通过随机特征图分解来表达. 他们证明了任意注意力矩阵都可以通过随机特征实现有效近似, 并通过使用positive random features(正向随机特征)进行了实现. Performer显著改善了传统transformer的时间和空间复杂度, 在保证性能的前提下可以使模型在处理更长序列的同时实现更高效的训练。

      Reservoir transformer与Performer的成功使我们意识到, 在各种神经网络以及深度学习架构中通过引入RC这种随机的思想, 都可能对网络性能和计算效率有一定的改善, 对于不同的网络架构, 如何引入这种随机性还有待研究人员的进一步探索。

7.未来研究方向

      我们给出一些当前RC尚未解决或值得探索的问题以供大家探讨。

    （1）隐藏层(reservoir)可用于动力系统学习和预测的的动力学机制还不清楚;

    （2）层次结构和结构化拓扑对RC性能的影响有待进一步探索;

    （3）如何克服储备池产生的随机性, 构造一个具体问题最优的RC网络结构, 即增强RC的可塑性问题;

    （4）如何通过在深度神经网络中加入类似于RC的随机性结构使得网络性能和训练效率之间可以达到最优的平衡, 以及探索这种随机性发挥作用的理论原理。

文：赵伯林

参考文献

[1] H. Jaeger, The echo state approach to analysing and training recurrent neural networks —With an erratum note, Fraunhofer Institute for Autonomous Intelligent Systems, 2010.

[2] W. Maass, T. Natschläger, and H. Markram, Real-time computing without stable states: A new framework for neural computation based on perturbations, Neural Computation, 14(11):2531-2560, 2002.

[3] D. Verstraeten, B. Schrauwen, M. D’Haene, and D. Stroobandt, An experimental unification of reservoir computing methods, Neural Networks, 20(3):391-403, 2007.

[4] N. Soures and D. Kudithipudi, Spiking reservoir networks: brain-inspired recurrent algorithms that use random, fixed synaptic strengths, IEEE Signal Processing Magazine, 6(36):78-87, 2019.

[5] B. Schrauwen, D. Verstraeten, and J. Campenhout, An overview of reservoir computing: theory, applications and implementations, Proceedings of the 15th European Symposium on Artificial Neural Networks, 2007.

[6] A. Litwin-Kumar, K. D. Harris, R. Axel, H. Sompolinsky, and L. Abbott, Optimal degree of synapic connectivity, Neuron, 93(5):1153–1164, 2017.

[7] M. Lukoševičius, A practical guide to applying echo state networks, Neural Networks: Tricks of the Trade, New York: Springer, pp. 659-686, 2012.

[8] X. Han, Y. Zhao, and S. Micheal, Revisiting the memory capacity in reservoir computing of directed acyclic network, Chaos, 31(3):03310, 2021.

[9] B. Schrauwen, M. Wardemann, D. Verstraeten, and J. Steil, Improving reservoirs using intrinsic plasticity, Neurocomputing, 71(7-9):1159-1171, 2007.

[10] H. Paugam-Moisy, R. Martinez, and S. Bengio, Delay learning and polychronization for reservoir computing, Neurocomputing, 71(7-9):1143-1158, 2008.

[11] K. Bush and B. Tsendjav, Improving the richness of echo state features using next ascent local search, Artificial Neural Networks in Engineering Conferences, 2005.

[12] J. Triesch, A gradient rule for the plasticity of a neuron’s intrinsic excitability, International Conference on Artificial Neural Networks, 2005.

[13] J. Steil, Online reservoir adaptation by intrinsic plasticity for backpropagation-decorrelation and echo state learning, Neural Networks, 20(3):353-364, 2007.

[14] J. Boedecker, O. Obst, and N. Micheal, Studies on reservoir initialization and dynamics shaping in echo state networks, The 17th European Symposium on Artificial Neural Networks, 2009.

[15] H. Jaeger and H. Haas, Harnessing Nonlinearity: Predicting chaotic systems and saving energy in wireless communication, Science, 304(5667):78–80, 2004.

[16] J. Pathak, B. Hunt, M. Girvan, Z. Lu, and E. Ott, Model-free prediction of large spatiotemporally chaotic systems from data: a reservoir computing approach, Physical Review Letters, 120(2):024102, 2018.

[17] Q. Zhu, H. Ma, and W. Lin, Detecting unstable periodic orbits based only on time series: When adaptive delayed feedback control meets reservoir computing, Chaos, 29(9):93125-93125, 2019

[18] W. Lin and H. Ma, Failure of parameter identification based on adaptive synchronization techniques, Physical Review E, 75(6):066212, 2007.

[19] H. Ma and W. Lin, Nonlinear adaptive synchronization rule for identification of a large amount of parameters in dynamical models, Physical Review A, 374(2):161–168, 2009.

[20] W. Lin and H. Ma, Synchronization between adaptively coupled systems with discrete and distributed time-delays, IEEE Transactions on Automatic Control, 55(4):819–830, 2010.

[21] 彭宇, 王建民, 彭喜元, 储备池计算概述, 电子学报, 39(010):2387-239, 2011.

[22] M. Buehner and P. Young, A tighter bound for the echo state property, IEEE Transactions on Neural Networks, 17(2):820-824, 2006.

[23] N. M. Soures, Deep Liquid State Machines with Neural Plasticity and On-device Learning, M.S. thesis, Rochester Institute of Technology, 2017.

[24] L. Ribeiro , P. Saverese, and D. N. Figueiredo, Struc2vec: learning node representations from structural identity, The 23rd ACM SIGKDD International Conference, 2017.

[25] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, and A. N. Gomez, Attention is all you need, Advances in Neural Information Processing Systems, 2017.

[26] S. Shen, A. Baevski, A. Morcos, and K. keutzer, Reservoir transformers, unpublished manuscript.

[27] K. Choromanski, V. Likhosherstov, D. Dohan, X. Song, A. Gane, T. Sarlos, P. Hawkins, J. Davis, A. Mohiuddin, L. Kaiser, D. Belanger, L.Colwell, and A. Weller, Rethinking attention with performers, International Conference on Learning Representations, 2021