神经与电的关系

18世纪中叶，人们进行电学研究发现了电力对人体的影响，医用电学这一领域因而诞生。著名科学家路易吉·伽伐尼（Luigi Aloisio Galvani）对医用电学产生兴趣，他通过将两种不同的金属器械连接在一起，然后与解剖过的青蛙腿接触，意外地发现青蛙腿会发生颤动。这一发现与随后的一系列实验揭示了肌肉运动与电能的联系。伽伐尼提出了“动物电”（“生物电”）这一术语，用来描述激发他的标本肌肉产生运动的力量。伽伐尼认为，标本的肌肉活动是由神经带到肌肉的一股电流引发的。这个让肌肉产生颤动的神经信号后来被称为动作电位（action potential），也就是处于静止膜电位状态的细胞膜，在适当的刺激下产生的一种快速的跨膜电位变化。

然而，亚历山德罗·伏特（Alessandro Giuseppe Antonio Anastasio Volta）持有不同观点，他认为刺激的真正来源是不同种类金属的接触。他将通过这种方式产生的电称为“金属电”，并认为肌肉在接触金属时收缩类似于验电器的运作方式。为了推翻伽伐尼的“动物电”理论，伏特还特意发明了伏打堆：他认为所有原电池都有电动势；生物电和电化电池产生的电流的化学基础相同，因而“动物电”现象可在动物体外被复制。伏特还研究了我们现在所谓的电容，他研究了电势和电荷之间的关系，发现它们之间成正比，这被称为电容的伏打定律。为了纪念伏打，电势的单位被命名为伏特。尽管双方都未能对“生物电”做出正确的分析，但好的对手永远都是珍贵的：正是伽伐尼与伏特的争论推动了一系列开创性的实验，推进了电学和生物学的发展。

动作电位

自那时起，神经科学研究迎来了巨大的变革，科学家对神经传导和电信号之间的关系有了更深入的认识。他们发现了动作电位：当输入到神经细胞膜上的电流超过特定的阈值时，细胞膜外离子会突然加速流向胞内，随后沿着神经纤维传导出去；而小于阈值的电流则不会引发有效的信号传递（图一为产生动作电位时细胞膜电位随着时间的变化过程）。这种传导方式能够有效地抵抗干扰噪声，避免不必要的信息的产生和传递。

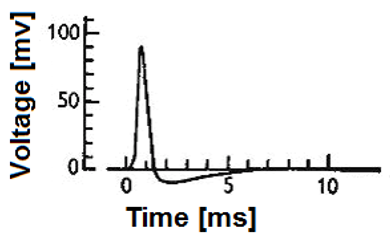
图一：在产生动作电位时，减去静息态电位的细胞膜电位随着时间的变化过程。动作电位的幅度和确切形状可以根据获取信号所用的确切实验技术而变化。（图源于：https://en.wikipedia.org/wiki/Biological_neuron_model）

生物神经元模型的产生

到了19世纪末，神经科学家开始使用电路来模拟神经元细胞膜上的现象。于是，刻画神经元细胞膜上产生的动作电位或尖峰（spike）的定量数学模型应运而生。其中，Alan Hodgkin和Andrew Huxley在1963年根据乌贼巨轴突的研究工作所建立动作电位的理论而共同获得诺贝尔奖。其著名的Hodgkin-Huxley模型准确描述了神经元动作电位的启动和传播。典型的Hodgkin-Huxley模型是一个连续的时间系统，将可兴奋细胞的每个组件都视为一个电元件，描述为一组非线性微分方程。该模型的优点是可以高度准确地再现电生理学结果，但它的复杂性较高，一些参数值在实验中较难测得。因此，既保留了部分电生理特性（放电时间），又相对简单易测的整合-发放（Integrate-and-fire）模型得以广泛应用。

非漏电整合-发放模型

早在1907年，路易·拉皮克（Louis Lapicque）提出了一条完美整合-发放模型（perfect integrate-and-fire model），也被称为非漏电整合-发放模型（non-leaky integrate-and-fire model），简写为perfect IF或non-leaky IF。他提出了该模型的数学方程式

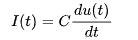
在给定输入电流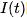的情况下，神经元的膜电位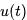会随时间发生如上所述的变化，完美符合电容定律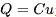关于时间的导数。当施加输入电流时，电压随时间逐渐增加，直到达到固定的阈值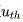。一旦达到阈值，会产生一个尖峰，类似于一个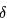函数的形状，并且电压会被重置回静息电位。然后模型会继续运行。因此，该模型的放电频率（firing frequency），即尖峰之间时间间隔的倒数，会随着输入电流的增加而无限制地线性增加。

该模型可以通过引入不应期（refractory period）来限制神经元的放电频率，从而使模型更加准确。对于恒定输入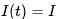，假设电压从零开始，经过时间后达到阈值电压。在复位之后，不应期引入一个神经元不发生放电的时间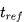，以确保下一次发射的总时间为。那么放电频率作为恒定输入电流的函数可以表示为

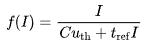
该模型的一个缺点是没有考虑细胞膜的泄漏（leakage）行为，即细胞膜并非完全绝缘，当电流输入时存在电荷的流失现象；另一个不符合观察到的神经元行为的特征是，如果该模型在某个时刻接收到一个低于阈值的短脉冲电流，它会一直保持电压的升高并永远保持在这个电位，直到后续的输入达到阈值才发生放电。然而，实际观察到的神经元行为并不会表现出这种持续的电压升高现象。因此，这些缺点限制了该模型的准确性，进一步的改进和扩展需要考虑泄漏行为以及与实际神经元行为更一致的特征。

漏电整合-发放模型

为了更精确地描述神经元的放电过程，科学家在基于非漏电整合-发放模型的基础上引入了“泄漏”项。当外部输入电流被施加时，多余的电荷被储存在包围神经元的细胞膜中，使细胞膜表现得像一个容量为C的电容器。然而，由于细胞体作为一个绝缘体并不完美，电荷会随着时间的推移通过细胞膜慢慢地泄漏。因此，细胞膜的泄漏行为可以通过引入漏电电阻R来描述。模型的基本电路由电流驱动，其中电容器C和电阻R并联（图二为漏电整合-发放模型的示意图）。此时，漏电整合-发放模型（leaky integrate-and-fire model，简写为LIF模型）中描述膜电位变化的表达式为

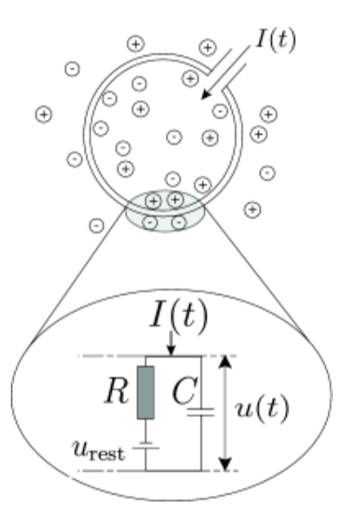
图二：被细胞膜（大圆）包围的神经元接收到（正）输入电流，这会增加细胞内的电荷。细胞膜的作用就像一个电容器，与电阻并联，电阻与电池串联。（图源于：Neuronal Dynamics）

在电阻R趋近无穷大的情况下，即细胞膜是完美绝缘体的情况下，得到非漏电整合-发放模型模型。对于该方程如果给定初值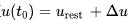，在没有外部输入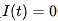的情况下，该方程的解为

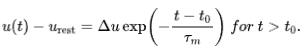
膜电位会指数衰减至静息电位。膜时间常数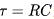是衰减的特征时间。特征时间越大，意味着膜电位变化越慢。上述方程解是在没有外部输入的情况下得到的，因此也被称为"自由"解。然而，当考虑到外部输入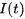时，衰减的特征时间也会受到外部输入大小的影响。外部输入越大，特征时间越小，膜电位变化速度越快。

由阈值准则定义神经元放电时间为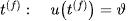，在放电时间之后，膜电位马上设置为新值（一般为静息电位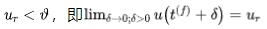），即（如图三所示，θ为阈值）。如果考虑加入不应期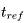，对于常值输入来说，触碰阈值的最小输入。假设电压触碰阈值重置为0，此时的放电频率为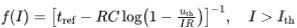。对于电流输入较大的情况，将会收敛到上述考虑不应期的非漏电整合-发放模型。

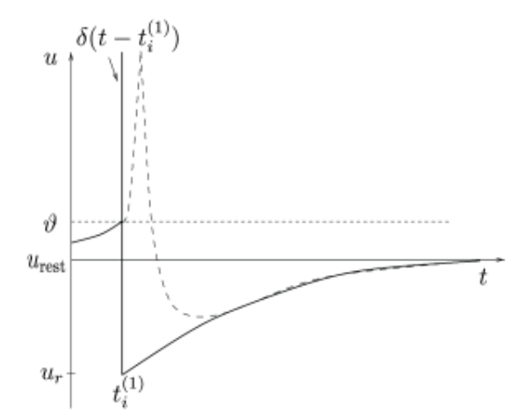
图三：在LIF模型中，动作电位的形状（虚线）通常用函数脉冲（竖线）代替。脉冲后的负电压 （尖峰后电位）被膜电位的“重置”值所取代。此时的脉冲放电时间为。（图源于：Neuronal Dynamics）

考虑到体内神经元活动的噪声特性，神经元通常接收复杂的时变输入。为了模拟这一点，研究模型常常将LIF神经元暴露于均值为，标准差为的高斯白噪声（Gauss White Noise，简写为GWN）。当以GWN均值或常值电流输入为自变量时，输出放电率（spike count）绘制的图像被称为神经元的输入-输出传递函数，也称为F-I曲线或增益曲线。常值输入的F-I曲线呈现非线性关系，而当高斯白噪声的标准差提升至一定数值时，可以观察到F-I曲线近似为一条直线（如图四所示）。这种线性关系的存在可以在一定程度上解释神经元的响应特性，也为模型计算的方便和进一步的理论研究提供了合理性。

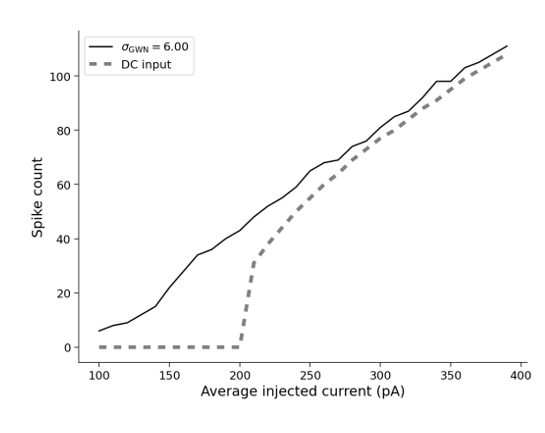
图四：LIF模型在高斯白噪声和常值电流下的输入-输出曲线（F-I曲线）。（图源于：https://compneuro.neuromatch.io/tutorials/W2D3_BiologicalNeuronModels/student/W2D3_Tutorial1.html）

然而，该模型仍然是高度简化的，忽略了神经元动力学的许多方面。特别是，该模型假设来自突触前神经元或其他外部电流注入的输入是线性积分的，并且与突触后神经元的状态无关。此外，在每个输出尖峰之后，膜电位被重置，因此不会保留之前尖峰的记忆，缺乏对神经元适应性（adaptation）的描述：即实验中发现即使将恒定电流注入体细胞，输出尖峰之间的时间间隔会自适应地改变。为了解决这些问题，研究人员建立了更多能够高度准确地预测电流注入神经元的尖峰时间的模型。其中一些模型包括自适应积分-发放模型（Adaptive integrate-and-fire model）、分数阶漏电积分-发放模型（Fractional-order leaky integrate-and-fire model）、指数积分-发放模型（Exponential integrate-and-fire model）等。这些模型在模拟神经元动力学方面更加精细，并且能够更好地捕捉到实验观察到的神经元响应特性，尤其是对于恒定输入电流的尖峰行为。

从生物物理学上较为准确的模型（Hodgkin-Huxley模型）到遍及现代深度学习各个方面的简单的人工神经元，LIF 神经元在各种各样的神经元模型中处于生物学合理性和实用性之间的位置（如图五所示）。LIF 神经元抽象出输出尖峰的形状和轮廓，将其视为离散事件。因此，信息并不存储在尖峰本身，而是存储在尖峰出现的时间（或频率）中。简化的尖峰神经元模型对神经编码、记忆、网络动力学以及最近基于Spiking Neuronal Network的深度学习研究方向产生了深远影响。

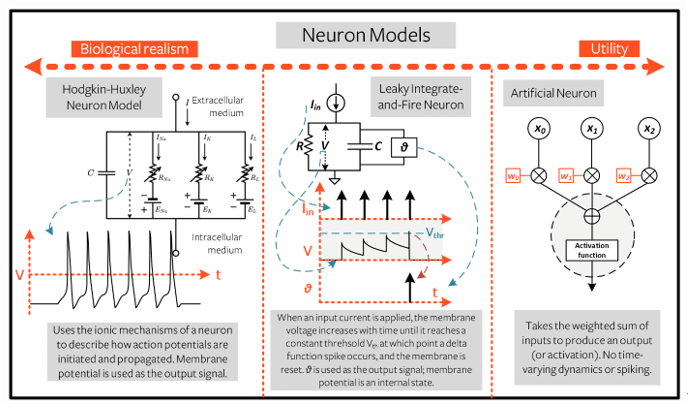
图五：相比于精确但复杂Hodgkin-Huxley模型和简单却灵活的人工神经元模型，LIF模型居于合理性与复杂性的中间位置（图源于：https://snntorch.readthedocs.io/en/latest/tutorials/tutorial_2.html）

尽管我们不能用类IF模型来完全解释神经元的生物化学和生物物理学特性，但当涉及到产生精确定时事件的峰值时，类IF模型表现出令人惊讶的准确性。因此，它可能是描述神经元产生尖峰活动的有效模型。一旦我们确定了合适的候选神经元模型，我们就可以利用这些模型构建大规模的神经元网络，并使用它们来理解神经元群体的动态和计算原理，以及可能的神经编码机制。虽然我们并不期待用类IF模型可以完全理解整个大脑，但从经过良好测试的简化神经元模型中理解大规模神经元网络的工作原理是一个较好的方式。例如，Binzegger等人1基于LIF模型研究了猫的V1视觉区连接结构对皮层信号处理的影响；Chaudhuri等人2采用了猫的V1视觉区数据作为模型的结构参数，基于Markov等人3提供的猕猴大脑皮层加权有向区域间连接性矩阵，进一步研究了由29个广泛分布的猕猴脑区组成的线性阈值循环网络系统中出现的时间尺度层次结构，该层次结构与区域功能相一致。这些研究表明，基于LIF模型的神经元和大规模神经网络的构建可以帮助我们更好地理解神经元群体的功能和动态。尽管仍面临挑战，但这种模型的应用有助于揭示神经系统的复杂性和计算原理。

参考资料：

1. Binzegger T, Douglas R J, Martin K A C. A quantitative map of the circuit of cat primary visual cortex[J]. Journal of Neuroscience, 2004, 24(39): 8441-8453.
2. Chaudhuri R, Knoblauch K, Gariel M A, et al. A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex[J]. Neuron, 2015, 88(2): 419-431.
3. Markov N T, Ercsey-Ravasz M M, Ribeiro Gomes A R, et al. A weighted and directed interareal connectivity matrix for macaque cerebral cortex[J]. Cerebral cortex, 2014, 24(1): 17-36.
4. Eshraghian J K. (2021) TUTORIAL 2 - THE LEAKY INTEGRATE-AND-FIRE NEURON. Retrieved May 29, 2023, from https://snntorch.readthedocs.io/en/latest/tutorials/tutorial_2.html
5. Gerstner W, Kistler W M, Naud R, et al. Neuronal dynamics: From single neurons to networks and models of cognition[M]. Cambridge University Press, 2014.
6. Biological neuron model. Retrieved May 29, 2023, from https://en.wikipedia.org/wiki/Biological_neuron_model
7. Gu Q, Li S, Murray J, et al.（2020）Tutorial 1: The Leaky Integrate-and-Fire (LIF) Neuron Model. Retrieved May 29, 2023, from https://compneuro.neuromatch.io/tutorials/W2D3_BiologicalNeuronModels/student/W2D3_Tutorial1.html
8. Guo G. (2013) 【探索10 】探索內心的小宇宙：談大腦的理論與模型. Retrieved May 29, 2023, from https://case.ntu.edu.tw/blog/?p=14711