什么是“熵”？ 

“熵”是一个乍看起来很怪的汉字，它也并不是古代就有的字，而是1923年中国物理学家胡刚复（1892-1966）教授翻译得出，根据其意义为热量与温度之商，并且与火（热）有关而命名。其德文原词“Entropie”是德国科学家克劳修斯（1822-1888）在1865年^[1]中提出的，刻意使之与能量（Energie）一词形似，以分别对应热力学第二定律和热力学第一定律；其英文翻译即为大家熟悉的“Entropy”。不过，熵不仅仅只有宏观意义，还有微观的统计力学解释，最早由玻尔兹曼（1844-1906）在1872年^[2]和1877的文章^[3]中提出。他将一个宏观物体的熵定义为和它对应的微观态的个数的对数成正比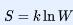：, 这里S代表熵，k是玻尔兹曼常数，W代表系统宏观状态所对应的微观状态数。该解释后又赋予熵以系统混乱度的量度这一物理意义。热力学第二定律由此得到一个微观解释：孤立系统的自发过程总是从热力学概率小的宏观状态向热力学概率大的宏观状态转变。

熵，不仅仅只和火有关 

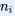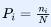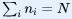19与20世纪，物理学家吉布斯（1839-1903）对熵的概念提出了新的理解^[4]。回想玻尔兹曼公式，通过系统的微观状态数来计算系统的熵，但每个状态的微观态数是一个疯狂的天文数字，无法直接测得。换种方式思考，假定一个系统可以有N种不同的等概率的微观态，这些微观态被分为n个不同的组，称为宏观态。第i个宏观态包含  个微观态，宏观态的所有微观态之和等于微观态的总数.。系统处于第i个宏观态的概率为，所以  以及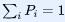 。由玻尔兹曼的公式可知整个系统的熵为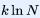，而这也等于系统 处于不同宏观态的熵 与 处在单个宏观态中的熵 的和；后者等于 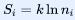 ; 因此系统处于不同宏观态的熵为  , 这就是知名的吉布斯熵公式。通过概率来计算熵，赋予了熵新的意义。好的思想总是简单优美又具有延展性。半个多世纪后，香农（1916-2001）重新写下同一个公式^[5]，但将熵理解为信息的量度，抑或是不确定性的量度。简单解释之，假设一个信息存在不同表述的概率为 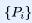。如果它被确定表述为一种方式，那么对应的 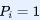, 其余 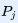 均为0，容易看出此时吉布斯-香农熵为0，即此时的不确定性为0。如果信息以不同的概率存在于不同的表述之中，那么信息熵就不为0，意即信息的表述包含了不确定性。顾名思义，这时的“熵”似乎应更改为“謪”，不过没见有人用这个字。香农的“简单”诠释开启了信息学这一新的科学分支。

极大熵，一个通用的原理

熵的意义还可以被继续拓展。数学家E. T. Jaynes（1922-1998）观察到了一个事实^[6]：统计力学中的两个经典概率分布，微正则系综（microcanonical ensemble）（即均匀分布），以及正则系综（canonical ensemble）（即，这里  是该宏观态的能量）都可以被理解为在特定约束下极大化玻尔兹曼-吉布斯-香农熵函数所得到的解。前者服从于最简单的约束，即所有概率分量  的和为1；后者服从于总能量期望值为定值的约束；接下来，只需简单应用Lagrange乘子法（以随机变量  作为自变量），就可以分别解出微正则系综和正则系综两种概率分布。Jaynes建议将这个原理外推到所有的概率推断问题上。熵最大的概率分布解是所有被允许的解中含有最大不确定性的解，因此是包含最少人为偏见（mostly unbiased）的解，也就是最合理、可能性最大的解。Jaynes也说明这个原理不仅在平衡态统计力学中蕴含了玻尔兹曼与吉布斯的定理，也可以被应用于远非平衡的状态和各式各样的复杂系统。这被称为极大熵或者最大熵原理（Maximum Entropy Principle）。

无处不在的极大熵？ 

在过去的几十年里，大数据科学得到了迅猛的增长，也推进了人工智能、机器学习的进步。然而，真正复杂的系统，例如生态系统、经济和气候，因其系统变量过多，不确定性很大，通过已知信息对这样的系统进行建模不足以确定结果，甚至还有无数人们知之甚少的隐藏机制，或者边界条件不足以唯一确定解的轨迹。对于这样具有不完全信息的系统，我们如何预测其行为？答案是转向信息论，特别是，这篇文章所介绍的极大熵推理过程。基本思想是将我们想要做出推断的变量作为随机变量，利用我们所获得的信息和知识作为约束条件，然后通过最大化某个熵函数来获得额外的知识。从Jaynes以来，极大熵原理已经被运用于多种关于复杂系统的领域，包括但不限于图像处理、时间序列分析、资讯存储、马尔可夫链、资讯分解、物种产生与消灭、蛋白质折叠、医药与疾病的因果关系、集体行为分析、生物网络、神经网络、层次结构树网络、社会结构、社会经济学、博弈论、交通系统、分子反应动力学、量子系统等^[7]。虽然有着多种多样的应用，但极大熵本身就是一个解决大量问题一般逻辑的基础。

参考文献 

[1] Rudolf Julius Emanuel Clausius, Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie, 1865 .
[2] Ludwig Eduard Boltzmann, Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen, 1872 .[3] Ludwig Eduard Boltzmann, Über die Beziehung eines allgemeine mechanischen Satzes zum zweiten Hauptsatze der Warmetheorie, 1877.
[4] Josiah Willard Gibbs, Elementary Principles in Statistical Mechanics, developed with especial reference to the rational foundation of thermodynamics, 1902 .
[5] Claude Elwood Shannon, A Mathematical Theory of Communication, 1948.
[6] Edwin Thompson Jaynes, Information Theory and Statistical Mechanics, 1957.
[7] John Hatte & Amos Golan, Information theory: A foundation for complexity science, 2022.