搜索

本系列文章将解读Allison J. Lopatkin 和 James J. Collins 2020年发表在《Nature Reviews Microbiology》上的文章《Predictive biology: modelling,understanding and harnessing microbial complexity》,聚焦生物系统潜在动力学预测的需要,侧重生物系统在建模过程中遇到的挑战,关心生命活动中的各种震荡行为与其成因[1]。
预测生物学是继合成生物学和系统生物学之后的伟大篇章,特别是对微生物而言。以往,生物学家们在研究一个问题时,最常用的手段即进行生物学实验,从而有了海量的实验数据。学者利用这些数据总结规律,发现基因与蛋白质的关系、发现疾病与特定物质的关系。这些数据是实验性与经验性的产物,是过去的总结,也是不可再复制的昨天。
因此,预测生物学诞生了——利用数据以预测未来。
在海量数据面前,深度学习等“黑匣子”工具非常有吸引力。那么为什么预测生物学仍然需要建立数学模型呢?这主要是因为机器学习模型容易出现过度拟合,偏差和无法解释的情况,从而导致模型结构难以在体外进行验证,缺乏预测价值。因此,生物系统潜在动力学的数学模型研究的重要性仍然不可忽略,其应该被视为新兴技术的一种重要补充方法。
现实的情况也是如此。大型游戏公司会根据用户信息对可疑“欺骗”用户进行预测、基于路况预测的自动驾驶技术也已经投入现实生活中使用,尽管预测分析技术已经完全改变了我们的生活,但在过去的几十年中,生物学似乎并没有按照我们的希望落入这一范式中。例如,大肠杆菌(Escherichia coli)是最典型的模型的生物之一,其具有超过二十年的完整测序和全面注释的基因组。然而,截至2019年,大肠杆菌中约35%的蛋白质编码基因的功能仍然处于未知状态。这也意味着预测生物学中仍然有很多亟待解决的问题。
在动力学建模的过程中,必不可缺的是对生物系统的理解与抽象。一般来说,通过实验统计亦或是机器学习的方法,只能看到某些现象及规律,不一定能够看到其本质,也不能很好地解释生物体中的各种运行机制并在此基础上进行预测和调控。
因此,合理、可解释的数学模型特别适合解决这些需求。因此,本篇文章首先简要介绍生物学中的动力学系统建模。在后续的文章中,我们再从生物复杂性不断增加的背景下检查建模的有效性,首先是从较低级别的细胞过程开始,然后发展到社区/网络级别的生态和进化动力学。同时,我们也将穿插介绍一些生物学中经典的模型与近期的研究,进行分析与探讨,以一系列的关键例子强调生物系统潜在动力学的迫切需要。
预测生物学中几种经典的模型
数学模型的目的是以精确和定量的方式描述一个或多个目标变量。最简单的情况下,我们用一个线性方程()来刻画变量y随着变量x线性改变的关系。其中,,是拟合参数,根据数据来确定,然而,由于这些参数不一定具有生物学意义,因此细胞水平或分子水平的模型通常来自生化“第一原理”(first principles)。也即模型的探索应该建立在生化反应的基础准则上,各个变量应有其对应的现实意义或具有说服力的假设。
根据各种变量以及模型设计的准则,John J. Tyson等人将基本模型按下表进行分类[2],它们也构成了生物系统动力学模型中的标准组件(standard component)。对于确定性模型而言,我们将其分为离散模型与连续模型。这里将离散模型分为了布尔类型与分段线性模型,离散量的产生或许与电位变化与阈值等电生理信号或振荡状态相关。最广为研究和关注的是连续模型,一组常微分方程(ODEs)刻画了变量随时间和其他变量连续改变的过程。例如,这里介绍一个经典的Michaelis-Menten模型:
在酶的催化作用下,底物()将转换为产物(),产物的变化率()与底物的浓度有关,却不是简单的线性关系,表示酶最大催化速率,是达到最大速率一半的底物浓度,t是时间(实际上,这是时的Hill function)。这时,和就可以通过测量到的数据进行处理得到,其现实意义是非常充分的。
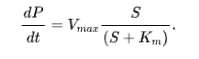
随机性模型是在确定性模型的基础上加上了噪声影响。噪声的来源是多方面的,有可能来自于测量手段限制或者来自于未考虑到的变量,当然,也有可能是来自生物内部,例如突变或者空间分布不均匀等。从现实的角度出发,随机性模型才是一种更为精确的模型,但对于理论研究来说,噪声项的加入可能反而会带来一些困扰,这其中也需要研究人员一定的取舍。
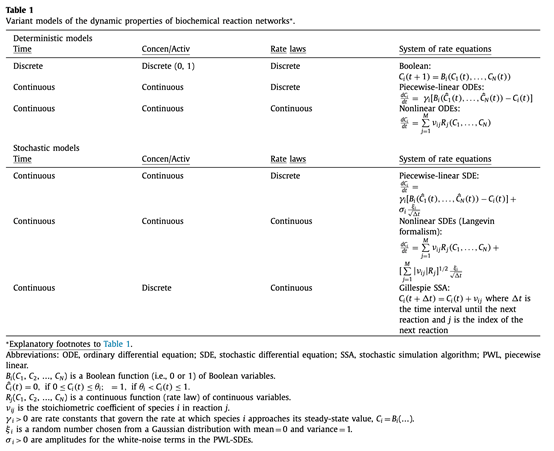
图 - 生化反应模型分类
另外,偏微分方程(PDEs)同样常被用以描述生物学行为。其实际意义在于,在考量变量随时间变化的同时,还将考虑变量随空间位置改变而产生的变化。比较经典的例子是二维的FitzHugh-Nagumo神经元模型(可视其为四维Hodgkin-Huxley神经元模型的简化):
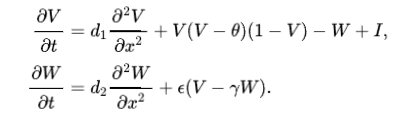
当确定了适合的数学模型之后,一些生物学中经验性的现象就得以解释了。
一个经典的范例就是对生物系统中双稳态(bistability)的研究。在研究青蛙卵裂的过程中,科学家注意到,随着信号强度的慢慢增加,细胞对信号的反应会在某个临界点从状态A突然跳跃至状态B。以及,原核生物的耐药性现象、大肠杆菌乳糖代谢活性的all-or-none现象等,也都有所谓的状态突变现象,并且随着参数的逆向改变,生物学家发现,正向突变与反向突变的节点并不是相同的,该双稳态现象的信号-响应(Signal-Response)曲线如下图右下角所示[3],箭头代表响应随信号改变的方向。而数学模型精妙解释了这种现象,这其实与分岔理论中的鞍结分岔(saddle-node bifurcation)有关,实际的参数-变量曲线(S形)应该如左下角所示。由于变量曲线中“拐点”的存在,在参数变化到临界值的时候,就产生了所谓的突变现象,同样这也说明了反向突变的合理性。
在下一期,我们将放缓脚步,先观察两个经典的基因合成网络,直观感受建模的魅力。
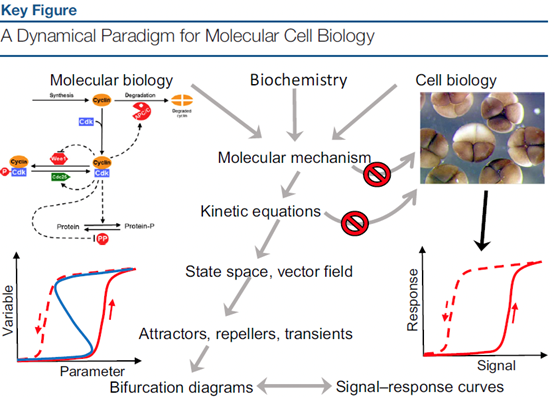
图 - 分子生物动力学
文:仲昭月
【参考文献】
[1]Lopatkin, A.J. and J.J. Collins, Predictive biology: modelling, understanding and harnessing microbial complexity. Nature Reviews Microbiology, 2020. 18: p. 507-520.
[2]Tyson, J.J., T. Laomettachit, and P. Kraikivski, Modeling the dynamic behavior of biochemical regulatory networks. Journal of Theoretical Biology, 2019. 462: p. 514-527.
[3]Tyson, J.J. and B. Novak, A dynamical paradigm for molecular cell biology. Trends in Cell Biology, 2020.


 loading......
loading......